
【题目】选修4-4:坐标系与参数方程
已知过点![]() 的直线
的直线![]() 的参数方程是
的参数方程是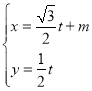 (
(![]() 为参数).以平面直角坐标系的原点为极点,
为参数).以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程式为
的极坐标方程式为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如表:
酒精含量(mg/100ml) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70)[] | [70,80) | [80,90) | [90,100] |
人数 | 3 | 4 | 1 | 4 | 2 | 3 | 2 | 1 |
(Ⅰ)绘制出检测数据的频率分布直方图(在图中用实线画出矩形框即可);
(Ⅱ)求检测数据中醉酒驾驶的频率,并估计检测数据中酒精含量的众数、平均数.
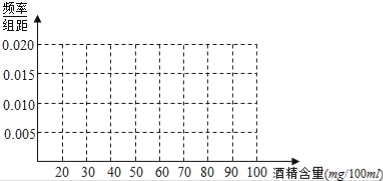
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把离心率![]() 的双曲线
的双曲线![]() 称为黄金双曲线.给出以下几个说法:
称为黄金双曲线.给出以下几个说法:
①双曲线![]() 是黄金双曲线;
是黄金双曲线;
②若双曲线上一点![]() 到两条渐近线的距离积等于
到两条渐近线的距离积等于![]() ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;
③若![]() 为左右焦点,
为左右焦点,![]() 为左右顶点,
为左右顶点,![]() 且
且![]() ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;
④.若直线![]() 经过右焦点
经过右焦点![]() 交双曲线于
交双曲线于![]() 两点,且
两点,且![]() ,
,![]() ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;
其中正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,且满足
两点,且满足![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点.
两点. ![]() 为坐标原点,若
为坐标原点,若![]() 的面积为
的面积为![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①所示,四边形![]() 为等腰梯形,
为等腰梯形,![]() ,且
,且![]() 于点
于点![]() 为
为![]() 的中点.将
的中点.将![]() 沿着
沿着![]() 折起至
折起至![]() 的位置,得到如图②所示的四棱锥
的位置,得到如图②所示的四棱锥![]() .
.
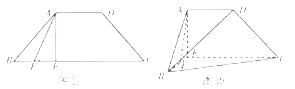
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费,为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(1)求直方图中![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用量不低于3吨的人数,并说明理由;
(3)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|-1≤x≤2},B={x|m-1≤x≤2m+1},已知BA.
(1)当x∈N时,求集合A的子集的个数;
(2)求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com