Question

5、若方程lnx+2x-10=0的唯一解为x₀，且x₀∈（k，k+1），k∈N，则k=

4

．

Answer 1

分析：先转化为两个简单函数判断交点所在区间的大致范围，再由零点判定定理确定即可．

解答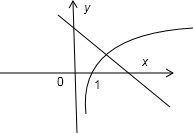：解：∵lnx+2x-10=0
∴lnx=10-2x，令g（x）=lnx，h（x）=10-2x在同一坐标系画出图象可得
由图可知x₀＞1，令f（x）=lnx+2x-10，
∵f（1）f（2）=-8（ln2-6）＞0，
f（2）f（3）=（ln2-6）（ln3-4）＞0，
f（3）f（4）=（ln3-4）（ln4-2）＞0，
f（4）f（5）=（ln4-2）ln5＜0，
可知k=4，
故答案为：4．

点评：本题主要考查函数零点所在区间的求法--图象法和零点判定定理．将函数的零点问题转化为两个函数交点的问题是常用的手段．