
【题目】已知递增数列![]() 共有2019项,且各项均不为零,
共有2019项,且各项均不为零,![]() ,若从数列
,若从数列![]() 中任取两项
中任取两项![]() ,
,![]() ,当
,当![]() 时,
时,![]() 仍是数列
仍是数列![]() 中的项,则数列
中的项,则数列![]() 中的各项和
中的各项和![]() ______.
______.
【答案】1010
【解析】
递增数列{an}共有2019项,且各项均不为零,a2019=1,可得0<a1<a2<…<a2019<a2019=1,因此0<a2019﹣a2018<a2019﹣a2017<…<a2019﹣a1<1,根据上述每项均在数列{an}中,可得a2019﹣a2018=a1,a2019﹣a2017=a2,…,a2019﹣a1=a2018,进而得出答案.
∵递增数列{an}共有2019项,且各项均不为零,a2019=1,
∴0<a1<a2<…<a2018<a2019=1,
∴0<a2019﹣a2018<a2019﹣a2017<…<a2019﹣a1<1,
且上述每项均在数列{an}中,
∴a2019﹣a2018=a1,
a2019﹣a2017=a2,
…,
a2019﹣a1=a2018.
即a2018+a1=a2017+a2=…=a1+a2018=a2019=1.
数列{an}的各项和2S2019=2019+1.
S2019=1010.
故答案为:1010.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的方程为
的方程为![]() ,其中常数
,其中常数![]() ,
,![]() 是抛物线
是抛物线![]() 的焦点.
的焦点.
(1)若直线![]() 被抛物线
被抛物线![]() 所截得的弦长为6,求
所截得的弦长为6,求![]() 的值;
的值;
(2)设![]() 是点
是点![]() 关于顶点
关于顶点![]() 的对称点,
的对称点,![]() 是抛物线
是抛物线![]() 上的动点,求
上的动点,求![]() 的最大值;
的最大值;
(3)设![]() ,
,![]() 、
、![]() 是两条互相垂直,且均经过点
是两条互相垂直,且均经过点![]() 的直线,
的直线,![]() 与抛物线
与抛物线![]() 交于点
交于点![]() 、
、![]() ,
,![]() 与抛物线
与抛物线![]() 交于点
交于点![]() 、
、![]() ,若点
,若点![]() 满足
满足![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD//BC,BC=2AD,AD⊥CD,PD⊥平面ABCD,E为PB的中点.
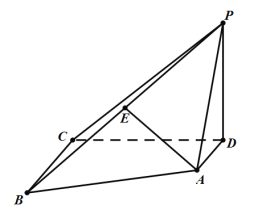
(1)求证:AE//平面PDC;
(2)若BC=CD=PD,求直线AC与平面PBC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年中秋节到来之际,某超市为了解中秋节期间月饼的销售量,对其所在销售范围内的1000名消费者在中秋节期间的月饼购买量![]() 单位:
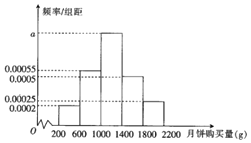
单位:![]() 进行了问卷调查,得到如下频率分布直方图:
进行了问卷调查,得到如下频率分布直方图:
![]() 求频率分布直方图中a的值;
求频率分布直方图中a的值;
![]() 以频率作为概率,试求消费者月饼购买量在
以频率作为概率,试求消费者月饼购买量在![]() 的概率;
的概率;
![]() 已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的
已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的![]() ,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求
,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求![]() 频率分布直方图中同一组的数据用该组区间的中点值作代表
频率分布直方图中同一组的数据用该组区间的中点值作代表![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]()
![]() .
.
(1)若![]() 求函数
求函数![]() 的单调区间;
的单调区间;
(2)若![]() 试判断函数
试判断函数![]() 在区间
在区间![]() 内的极值点的个数,并说明理由;
内的极值点的个数,并说明理由;
(3)求证:对任意的正数a都存在实数t满足:对任意的![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com