
设有一张边长为48cm的正方形铁皮 ,从其四个角各截去一个大小相同的小正方形 ,然后将剩余部分折成一个无盖的长方体盒子 ,所得盒子的体积V是关于截去的小正方形的边长x的函数 .
(1)随着x的变化 ,盒子体积V是如何变化的?
(2)截去的小正方形的边长x为多少时 ,盒子的体积最大?最大体积是多少?
(1)V = x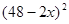 ,定义域为0 <x<24
,定义域为0 <x<24
(2)当截取的小正方形的边长为8cm时 ,得到的盒子体积最大 ,且最大体积为8192
【解析】解 :(1)有题意可得V关于x的函数解析式为
V = x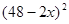 ,
,
定义域为0 <x<24 ,
 =
= 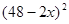 -4 x
-4 x =
12(x-8)(x-24),
=
12(x-8)(x-24),
当x∈(0 ,8)时体积V单调递增 ,x∈(8 ,24)时体积V单调递减 ;
(2)由(1)知 ,x = 8时 ,体积V有极大值 ,且唯一 ,那么x = 8时体积V有最大值 ,
最大值 = V(8) =
8192( ),
),
即当截取的小正方形的边长为8cm时 ,得到的盒子体积最大 ,且最大体积为8192 .
.


科目:高中数学 来源: 题型:
64
| ||
| 3 |
64
| ||
| 3 |

查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省高三第一次月考理科数学试卷(解析版) 题型:填空题
将一张边长为12cm的纸片按如图1所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折成一个有底的正四棱锥模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则四棱锥的体积是___________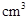 .
.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市海淀区高三5月查漏补缺数学试卷(解析版) 题型:填空题
将一张边长为12cm的纸片按如图1所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折成一个有底的正四棱锥模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则四棱锥的体积是___________ .
.

查看答案和解析>>
科目:高中数学 来源:2014届江苏省淮安市高一第一学期期末考试数学试卷 题型:解答题
(本题满分16分)如图所示,在一张边长为20cm的正方形铁皮的4个角上,各剪去一个边长是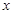 cm的小正方形,折成一个容积是
cm的小正方形,折成一个容积是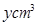 的无盖长方体铁盒,试写出用
的无盖长方体铁盒,试写出用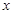 表示
表示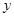 的函数关系式,并指出它的定义域。
的函数关系式,并指出它的定义域。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com