
°ĺŐ‚ńŅ°Ņ√ŅńÍĶń![]() ‘¬
‘¬![]() »’ «»ęĻķįģ—ņ»’£¨ő™Ńň”≠Ĺ”’‚“ĽĹŕ»’£¨ń≥Ķō«Ýőņ…ķ≤Ņ√Ň≥…ŃĘŃňĶų≤ť–°◊ť£¨Ķų≤ť°į≥£≥‘Ń„ ≥”ŽĽľ»£≥›ĶńĻōŌĶ°Ī£¨∂‘ł√Ķō«Ý–°—ßŃýńÍľ∂
»’ «»ęĻķįģ—ņ»’£¨ő™Ńň”≠Ĺ”’‚“ĽĹŕ»’£¨ń≥Ķō«Ýőņ…ķ≤Ņ√Ň≥…ŃĘŃňĶų≤ť–°◊ť£¨Ķų≤ť°į≥£≥‘Ń„ ≥”ŽĽľ»£≥›ĶńĻōŌĶ°Ī£¨∂‘ł√Ķō«Ý–°—ßŃýńÍľ∂![]() √Ż—ß…ķĹÝ––ľž≤ť£¨įīĽľ»£≥›Ķń≤ĽĽľ»£≥›∑÷ņŗ£¨Ķ√Ľ„◊‹ żĺ›£ļ≤Ľ≥£≥‘Ń„ ≥«“≤ĽĽľ»£≥›Ķń—ß…ķ”–
√Ż—ß…ķĹÝ––ľž≤ť£¨įīĽľ»£≥›Ķń≤ĽĽľ»£≥›∑÷ņŗ£¨Ķ√Ľ„◊‹ żĺ›£ļ≤Ľ≥£≥‘Ń„ ≥«“≤ĽĽľ»£≥›Ķń—ß…ķ”–![]() √Ż£¨≥£≥‘Ń„ ≥Ķę≤ĽĽľ»£≥›Ķń—ß…ķ”–
√Ż£¨≥£≥‘Ń„ ≥Ķę≤ĽĽľ»£≥›Ķń—ß…ķ”–![]() √Ż£¨≤Ľ≥£≥‘Ń„ ≥Ķ꼾żx≥›Ķń—ß…ķ”–
√Ż£¨≤Ľ≥£≥‘Ń„ ≥Ķ꼾żx≥›Ķń—ß…ķ”–![]() √Ż£ģ
√Ż£ģ
£®1£©ÕÍ≥…īūĺŪ÷–Ķń![]() Ń–Ń™ĪŪ£¨ő £ļń‹∑Ů‘ŕ∑łīŪ¬ ≤Ľ≥¨Ļż
Ń–Ń™ĪŪ£¨ő £ļń‹∑Ů‘ŕ∑łīŪ¬ ≤Ľ≥¨Ļż![]() Ķń«įŐŠŌ¬£¨»Ōő™ł√Ķō«Ý—ß…ķĶń≥£≥‘Ń„ ≥”ŽĽľ»£≥›”–ĻōŌĶ£Ņ
Ķń«įŐŠŌ¬£¨»Ōő™ł√Ķō«Ý—ß…ķĶń≥£≥‘Ń„ ≥”ŽĽľ»£≥›”–ĻōŌĶ£Ņ
£®2£©![]() √Ż«Ýőņ…ķ≤Ņ√ŇĶńĻ§◊ų»ň‘ĪňśĽķ∑÷≥…ŃĹ◊ť£¨√Ņ◊ť
√Ż«Ýőņ…ķ≤Ņ√ŇĶńĻ§◊ų»ň‘ĪňśĽķ∑÷≥…ŃĹ◊ť£¨√Ņ◊ť![]() »ň£¨“Ľ◊ťłļ‘ū żĺ› ’ľĮ£¨ŃŪ“Ľ◊ťłļ‘ū żĺ›ī¶ņŪ£¨«ůĻ§◊ų»ň‘Īľ◊∑÷ĶĹłļ‘ū ’ľĮ żĺ›◊ť£¨Ļ§◊ų»ň‘Ī““∑÷ĶĹłļ‘ū żĺ›ī¶ņŪ◊ťĶńłŇ¬ £ģ
»ň£¨“Ľ◊ťłļ‘ū żĺ› ’ľĮ£¨ŃŪ“Ľ◊ťłļ‘ū żĺ›ī¶ņŪ£¨«ůĻ§◊ų»ň‘Īľ◊∑÷ĶĹłļ‘ū ’ľĮ żĺ›◊ť£¨Ļ§◊ų»ň‘Ī““∑÷ĶĹłļ‘ū żĺ›ī¶ņŪ◊ťĶńłŇ¬ £ģ
łĹ£ļ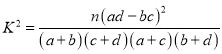
|
|
|
|
|
|
|
|
°ĺīūįł°Ņ£®1£©ŐÓĪŪľŻĹ‚őŲ,ń‹‘ŕ∑łīŪ¬ ≤Ľ≥¨Ļż0.001Ķń«įŐŠŌ¬£¨»Ōő™ł√Ķō«Ý—ß…ķĶń≥£≥‘Ń„ ≥”ŽĽľ»£≥›”–ĻōŌĶ£®2£©![]()
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›Ő‚÷––ŇŌĘÕÍ…∆![]() Ń–Ń™ĪŪ£¨≤Ęľ∆ň„≥Ų
Ń–Ń™ĪŪ£¨≤Ęľ∆ň„≥Ų![]() ĶńĻŘ≤‚÷Ķ£¨≤ĘĹęĻŘ≤‚÷Ķ”Ž
ĶńĻŘ≤‚÷Ķ£¨≤ĘĹęĻŘ≤‚÷Ķ”Ž![]() ĹÝ––īů–°Ī»ĹŌ£¨Ņ…∂‘Ő‚÷–ĹŠ¬ŘĶń’żőůĹÝ––Ň–∂Ō£Ľ
ĹÝ––īů–°Ī»ĹŌ£¨Ņ…∂‘Ő‚÷–ĹŠ¬ŘĶń’żőůĹÝ––Ň–∂Ō£Ľ
£®2£©Ĺęňý”–Ņ…ń‹∑÷◊ťĶń«ťŅŲŃ–ĺŔ≥Ųņī£¨»∑∂®»ę≤ŅĶń∑÷◊ť ż£¨≤Ę»∑∂® ¬ľĢ°įĻ§◊ų»ň‘Īľ◊∑÷ĶĹłļ‘ū ’ľĮ żĺ›◊ť£¨Ļ§◊ų»ň‘Ī““∑÷ĶĹłļ‘ū żĺ›ī¶ņŪ◊ť°ĪňýįŁļ¨Ķń◊ť ż£¨»ĽļůņŻ”√ĻŇĶšłŇ–ÕĶńłŇ¬ Ļę ĹŅ…ľ∆ň„≥Ųňý«ů ¬ľĢĶńłŇ¬ .
£®1£©”…Ő‚“‚Ņ…Ķ√Ń–Ń™ĪŪ£ļ
≤Ľ≥£≥‘Ń„ ≥ | ≥£≥‘Ń„ ≥ | ◊‹ľ∆ | |
≤ĽĽľ»£≥› |
|
|
|
Ľľ»£≥› |
|
|
|
◊‹ľ∆ |
|
|
|
![]() £¨
£¨
Ļ ń‹‘ŕ∑łīŪ¬ ≤Ľ≥¨Ļż![]() Ķń«įŐŠŌ¬£¨»Ōő™ł√Ķō«Ý—ß…ķĶń≥£≥‘Ń„ ≥”ŽĽľ»£≥›”–ĻōŌĶ£Ľ
Ķń«įŐŠŌ¬£¨»Ōő™ł√Ķō«Ý—ß…ķĶń≥£≥‘Ń„ ≥”ŽĽľ»£≥›”–ĻōŌĶ£Ľ
£®2£©…Ť∆šňŻĻ§◊ų»ň‘Īő™ĪŻļÕ∂°£¨
–°◊ť |
|
|
|
|
|
|
’ľĮ żĺ› | ľ◊““ | ľ◊ĪŻ | ľ◊∂° | ““ĪŻ | ““∂° | ĪŻ∂° |
ī¶ņŪ żĺ› | ĪŻ∂° | ““∂° | ““ĪŻ | ľ◊∂° | ľ◊ĪŻ | ľ◊““ |
∑÷◊ťĶń«ťŅŲ◊‹Ļ≤”–![]() ÷÷£¨
÷÷£¨
Ļ§◊ų»ň‘Īľ◊łļ‘ū ’ľĮ żĺ›«“Ļ§◊ų»ň‘Ī““łļ‘ūī¶ņŪ żĺ›’ľ![]() ◊ť£¨∑÷Īū «Ķŕ
◊ť£¨∑÷Īū «Ķŕ![]() ◊ťļÕĶŕ
◊ťļÕĶŕ![]() ◊ť.
◊ť.
ňý“‘Ļ§◊ų»ň‘Īľ◊∑÷ĶĹłļ‘ū ’ľĮ żĺ›◊ť£¨Ļ§◊ų»ň‘Ī““∑÷ĶĹłļ‘ū żĺ›ī¶ņŪ◊ťĶńłŇ¬ ![]() .
.



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ![]() ÷–£¨“—÷™Ķ„
÷–£¨“—÷™Ķ„![]() £¨
£¨![]() Ķń◊ÝĪÍ∑÷Īūő™
Ķń◊ÝĪÍ∑÷Īūő™![]() £¨
£¨![]() £ģ÷ĪŌŖ
£ģ÷ĪŌŖ![]() £¨
£¨![]() ŌŗĹĽ”ŕĶ„
ŌŗĹĽ”ŕĶ„![]() £¨«“ňŁ√«Ķń–Ī¬ ÷ģĽż «
£¨«“ňŁ√«Ķń–Ī¬ ÷ģĽż «![]() £ģľ«Ķ„
£ģľ«Ķ„![]() ĶńĻžľ£ő™
ĶńĻžľ£ő™![]() £ģ
£ģ
£®ĘŮ£©«ů![]() Ķń∑Ĺ≥Ő£ģ
Ķń∑Ĺ≥Ő£ģ
£®ĘÚ£©“—÷™÷ĪŌŖ![]() £¨
£¨![]() ∑÷ĪūĹĽ÷ĪŌŖ
∑÷ĪūĹĽ÷ĪŌŖ![]() ”ŕĶ„
”ŕĶ„![]() £¨
£¨![]() £¨Ļžľ£
£¨Ļžľ£![]() ‘ŕĶ„
‘ŕĶ„![]() ī¶Ķń«–ŌŖ”ŽŌŖ∂ő
ī¶Ķń«–ŌŖ”ŽŌŖ∂ő![]() ĹĽ”ŕĶ„
ĹĽ”ŕĶ„![]() £¨«ů
£¨«ů![]() Ķń÷Ķ£ģ
Ķń÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨‘ŕ![]() ÷–£¨
÷–£¨ ![]() £¨
£¨ ![]() ∑÷Īūő™
∑÷Īūő™![]() £¨
£¨ ![]() Ķń÷–Ķ„£¨
Ķń÷–Ķ„£¨![]() ő™
ő™![]() Ķń÷–Ķ„£¨
Ķń÷–Ķ„£¨![]() £¨
£¨![]() .Ĺę
.Ĺę![]() —ō
—ō![]() ’Ř∆ūĶĹ
’Ř∆ūĶĹ![]() ĶńőĽ÷√£¨ ĻĶ√∆Ĺ√ś
ĶńőĽ÷√£¨ ĻĶ√∆Ĺ√ś![]() ∆Ĺ√ś
∆Ĺ√ś![]() £¨»ÁÕľ2.
£¨»ÁÕľ2.
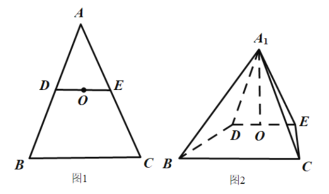
£®1£©«ů÷§£ļ![]() £Ľ
£Ľ
£®2£©«ů÷ĪŌŖ![]() ļÕ∆Ĺ√ś
ļÕ∆Ĺ√ś![]() ňý≥…Ĺ«Ķń’żŌ“÷Ķ.
ňý≥…Ĺ«Ķń’żŌ“÷Ķ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™∂®Ķ„![]() £¨
£¨![]() £¨÷ĪŌŖ
£¨÷ĪŌŖ![]() °Ę
°Ę![]() ŌŗĹĽ”ŕĶ„
ŌŗĹĽ”ŕĶ„![]() £¨«“ňŁ√«Ķń–Ī¬ ÷ģĽżő™
£¨«“ňŁ√«Ķń–Ī¬ ÷ģĽżő™![]() £¨ľ«∂ĮĶ„
£¨ľ«∂ĮĶ„![]() ĶńĻžľ£ő™«ķŌŖ
ĶńĻžľ£ő™«ķŌŖ![]() °£
°£
£®1£©«ů«ķŌŖ![]() Ķń∑Ĺ≥Ő£Ľ
Ķń∑Ĺ≥Ő£Ľ
£®2£©ĻżĶ„![]() Ķń÷ĪŌŖ”Ž«ķŌŖ
Ķń÷ĪŌŖ”Ž«ķŌŖ![]() ĹĽ”ŕ
ĹĽ”ŕ![]() °Ę
°Ę![]() ŃĹĶ„£¨ «∑Ůīś‘ŕ∂®Ķ„
ŃĹĶ„£¨ «∑Ůīś‘ŕ∂®Ķ„![]() £¨ ĻĶ√÷ĪŌŖ
£¨ ĻĶ√÷ĪŌŖ![]() ”Ž
”Ž![]() –Ī¬ ÷ģĽżő™∂®÷Ķ£¨»Űīś‘ŕ£¨«ů≥Ų
–Ī¬ ÷ģĽżő™∂®÷Ķ£¨»Űīś‘ŕ£¨«ů≥Ų![]() ◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…°£
◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…°£
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ…ŤÕ÷‘≤![]() Ķń◊ů°Ę”“∂•Ķ„∑÷Īūő™
Ķń◊ů°Ę”“∂•Ķ„∑÷Īūő™![]() £¨
£¨![]() £¨…Ō∂•Ķ„ő™B£¨”“ĹĻĶ„ő™F£¨“—÷™÷ĪŌŖ
£¨…Ō∂•Ķ„ő™B£¨”“ĹĻĶ„ő™F£¨“—÷™÷ĪŌŖ![]() Ķń«„–ĪĹ«ő™120°„£¨
Ķń«„–ĪĹ«ő™120°„£¨![]() .
.
(1)«ůÕ÷‘≤CĶń∑Ĺ≥Ő£Ľ
(2)…ŤPő™Õ÷‘≤C…Ō≤ĽÕ¨”ŕ![]() £¨
£¨![]() Ķń“ĽĶ„£¨Oő™◊ÝĪÍ‘≠Ķ„£¨ŌŖ∂ő
Ķń“ĽĶ„£¨Oő™◊ÝĪÍ‘≠Ķ„£¨ŌŖ∂ő![]() ĶńīĻ÷Ī∆Ĺ∑÷ŌŖĹĽ
ĶńīĻ÷Ī∆Ĺ∑÷ŌŖĹĽ![]() ”ŕMĶ„£¨ĻżM«“īĻ÷Ī”ŕ
”ŕMĶ„£¨ĻżM«“īĻ÷Ī”ŕ![]() Ķń÷ĪŌŖĹĽy÷Š”ŕQĶ„£¨»Ű
Ķń÷ĪŌŖĹĽy÷Š”ŕQĶ„£¨»Ű![]() £¨«ů÷ĪŌŖ
£¨«ů÷ĪŌŖ![]() Ķń∑Ĺ≥Ő.
Ķń∑Ĺ≥Ő.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ![]() ÷–£¨“—÷™Õ÷‘≤Ķń∑Ĺ≥Őő™£ļ
÷–£¨“—÷™Õ÷‘≤Ķń∑Ĺ≥Őő™£ļ![]() £¨∂ĮĶ„
£¨∂ĮĶ„![]() ‘ŕÕ÷‘≤…Ō£¨
‘ŕÕ÷‘≤…Ō£¨![]() ő™‘≠Ķ„£¨ŌŖ∂ő
ő™‘≠Ķ„£¨ŌŖ∂ő![]() Ķń÷–Ķ„ő™
Ķń÷–Ķ„ő™![]() .
.
£®1£©“‘![]() ő™ľęĶ„£¨
ő™ľęĶ„£¨![]() ÷ŠĶń’żįŽ÷Šő™ľę÷Š£¨Ĺ®ŃĘľę◊ÝĪÍŌĶ£¨«ůĶ„
÷ŠĶń’żįŽ÷Šő™ľę÷Š£¨Ĺ®ŃĘľę◊ÝĪÍŌĶ£¨«ůĶ„![]() ĶńĻžľ£Ķńľę◊ÝĪÍ∑Ĺ≥Ő£Ľ
ĶńĻžľ£Ķńľę◊ÝĪÍ∑Ĺ≥Ő£Ľ
£®2£©…Ť÷ĪŌŖ![]() Ķń≤ő ż∑Ĺ≥Őő™
Ķń≤ő ż∑Ĺ≥Őő™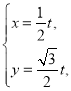 £®
£®![]() ő™≤ő ż£©£¨
ő™≤ő ż£©£¨![]() ”ŽĶ„
”ŽĶ„![]() ĶńĻžľ£ĹĽ”ŕ
ĶńĻžľ£ĹĽ”ŕ![]() °Ę
°Ę![]() ŃĹĶ„£¨«ůŌ“≥§
ŃĹĶ„£¨«ůŌ“≥§![]() .
.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ∆Ĺ√śňńĪŖ–ő![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() .
.
£®1£©«ů![]() ļÕňńĪŖ–ő
ļÕňńĪŖ–ő![]() Ķń√śĽż£Ľ
Ķń√śĽż£Ľ
£®2£©»ŰE «BDĶń÷–Ķ„£¨«ůCE.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™»żņ‚◊∂D°™ABCĶńňńłŲ∂•Ķ„‘ŕ«ÚOĶń«Ú√ś…Ō£¨»ŰAB£ĹAC£ĹBC£ĹDB£ĹDC£Ĺ1£¨ĶĪ»żņ‚◊∂D°™ABCĶńŐŚĽż»°ĶĹ◊Óīů÷Ķ Ī£¨«ÚOĶńĪŪ√śĽżő™(°°°°°°)
A. ![]() B. 2¶–C. 5¶–D.
B. 2¶–C. 5¶–D. ![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™Ķ„A£®©Ā2£¨1£©£¨B£®2£¨4£©£¨Ķ„P «÷ĪŌŖl£ļy£Ĺx…ŌĶń∂ĮĶ„.
£®1£©»ŰPA°ÕPB£¨«ůĶ„PĶń◊ÝĪÍ£Ľ
£®2£©…ŤĻżAĶń÷ĪŌŖl1”ŽĻżBĶń÷ĪŌŖl2ĺý∆Ĺ––”ŕl£¨«ůl1”Žl2÷ģľšĶńĺŗņŽ.
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com