
【题目】有下列说法: ①线性回归分析就是由样本点去寻找一条直线,使之贴近这些样本点的数学方法;②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示;③通过回归方程 ![]() ,可以估计和观测变量的取值和变化趋势;④因为由任何一组观测值都可以求得一个线性回归方程,所以没有必要进行相关性检验.其中正确命题的个数是( )
,可以估计和观测变量的取值和变化趋势;④因为由任何一组观测值都可以求得一个线性回归方程,所以没有必要进行相关性检验.其中正确命题的个数是( )
A.1
B.2
C.3
D.4
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(选修4-4 坐标系与参数方程) 以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为
轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为 (
(![]() 是参数),直线
是参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程和曲线C的普通方程;
的直角坐标方程和曲线C的普通方程;
(2)设点P为曲线C上任意一点,求点P到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班学生进行了三次数学测试,第一次有8名学生得满分,第二次有10名学生得满分,第三次有12名学生得满分,已知前两次均为满分的学生有5名,三次测试中至少有一次得满分的学生有15名,若后两次均为满分的学生至少有![]() 名,则
名,则![]() 的值为( )
的值为( )
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一条河的两岸平行,河的宽度d=600m,一艘客船从码头A出发匀速驶往河对岸的码头B.已知|AB|=1km,水流速度为2km/h, 若客船行驶完航程所用最短时间为6分钟,则客船在静水中的速度大小为( )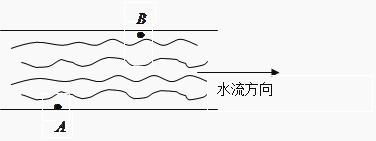
A.8km/h
B.![]() km/h
km/h
C.![]() km/h
km/h
D.10km/h
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|2x﹣1|+|x+1|,g(x)=|x﹣a|+|x+a|.
(Ⅰ)解不等式f(x)>9;
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2),求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义在R上的偶函数,对于x∈R,都有f(x+4)=f(x)+f(2)成立,当x1,x2∈[0,2]且x1≠x2时,都有![]() 给出下列四个命题:
给出下列四个命题:
①f(﹣2)=0;
②直线x=﹣4是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[4,6]上为减函数;
④函数y=f(x)在(﹣8,6]上有四个零点.
其中所有正确命题的序号为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC内接于☉O,AB=AC,直线MN切☉O于点C,弦BD∥MN,AC与BD相交于点E. 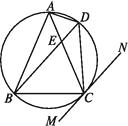
(1)求证:△ABE≌△ACD;
(2)求证:BE=BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com