
已知函数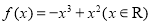 ,
,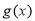 满足
满足 ,且
,且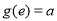 ,
,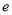 为自然对数的底数.
为自然对数的底数.
(1)已知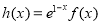 ,求
,求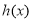 在
在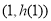 处的切线方程;
处的切线方程;
(2)若存在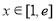 ,使得
,使得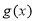
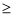
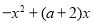 成立,求
成立,求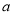 的取值范围;
的取值范围;
(3)设函数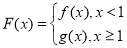 ,
,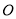 为坐标原点,若对于
为坐标原点,若对于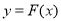 在
在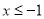 时的图象上的任一点
时的图象上的任一点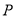 ,在曲线
,在曲线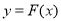
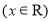 上总存在一点
上总存在一点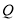 ,使得
,使得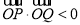 ,且
,且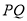 的中点在
的中点在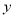 轴上,求
轴上,求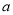 的取值范围.
的取值范围.
(1)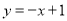 ;(2)
;(2)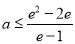 ;(3)
;(3)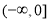 .
.
【解析】
试题分析:(1)应用导数的几何意义,求导数,求斜率,确定切线方程;
(2)由已知确定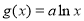 ;
;
根据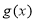
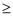
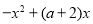 得:
得: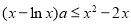 .
.
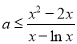 ,只需
,只需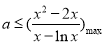 .
.
应用导数,求函数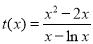 ,
,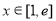 ,的最大值即得解;
,的最大值即得解;
(3)设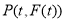 为
为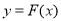 在
在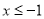 时的图象上的任意一点,可得
时的图象上的任意一点,可得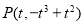 ,
,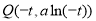 ,
,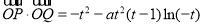 .
.
由于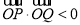 ,得到
,得到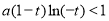 .
.
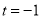 ,
, 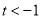 的情况,求得
的情况,求得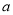 的取值范围.
的取值范围.
方法比较明确,分类讨论、转化与化归思想的应用,是解决问题的关键.
试题解析:(1)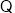
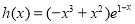 ,
,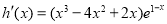
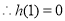 ,
,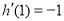

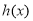 在
在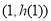 处的切线方程为:
处的切线方程为: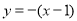 ,即
,即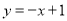 4分
4分
(2)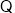
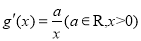 ,
,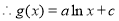
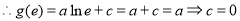 ,从而
,从而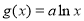 5分
5分
由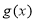
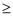
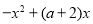 得:
得: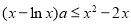 .
.
由于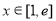 时,
时,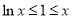 ,且等号不能同时成立,所以
,且等号不能同时成立,所以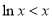 ,
,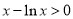 .
.
从而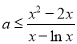 ,为满足题意,必须
,为满足题意,必须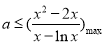 . 6分
. 6分
设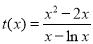 ,
,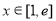 ,则
,则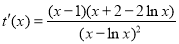 .
.
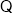
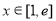 ,
,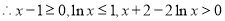 ,
,
从而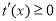 ,
,
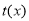 在
在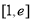 上为增函数,
上为增函数,
所以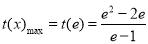 ,从而
,从而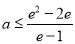 . 9分
. 9分
(3)设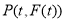 为
为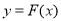 在
在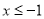 时的图象上的任意一点,则
时的图象上的任意一点,则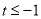
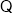
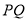 的中点在
的中点在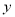 轴上,
轴上,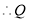 的坐标为
的坐标为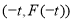 ,
,
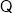
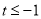 ,
,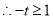 ,所以
,所以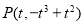 ,
,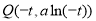 ,
,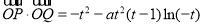 .
.
由于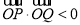 ,所以
,所以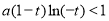 . 11分
. 11分
当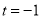 时,
时,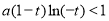 恒成立,
恒成立,
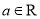 ; 12分
; 12分
当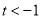 时,
时,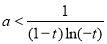 ,
,
令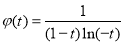
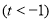 ,则
,则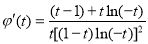
 ,
,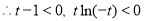 ,
,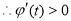 ,从而
,从而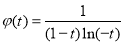 在
在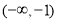 上为增函数,由于
上为增函数,由于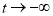 时,
时,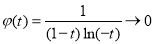 ,
,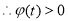 ,
,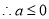
综上可知,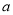 的取值范围是
的取值范围是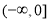 . 14分
. 14分
考点:应用导数研究函数的单调性、最(极)值,转化与化归思想,应用导数研究不等式恒成立问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)理科数学试卷(解析版) 题型:选择题
设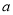 ,
,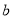 ,
,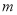 为整数(m>0),若
为整数(m>0),若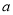 和
和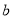 被
被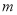 除得的余数相同,则称
除得的余数相同,则称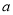 和
和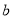 对模
对模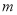 同余,记为
同余,记为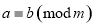 .若
.若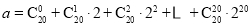 ,
, ,则
,则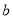 的值可以是( )
的值可以是( )
A.2011 B.2012 C.2013 D.2014
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)文科数学试卷(解析版) 题型:填空题
假设要考察某公司生产的500克袋装牛奶的三聚青氨是否超标,现从800袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第7行第8列的数开始向右读,则得到的第4个的样本个体的编号是 …(下面摘取了随机数表第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)文科数学试卷(解析版) 题型:选择题
一个几何体的三视图如图所示,其俯视图为正三角形,则这个几何体的体积为( )
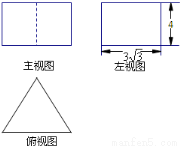
A.12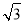 B.36
B.36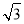 C.27
C.27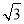 D.6
D.6
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省青岛市高三4月统一质量检测考试理科数学试卷(解析版) 题型:解答题
已知函数 ,
, .
.
(1)求函数 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)已知 中的三个内角
中的三个内角 所对的边分别为
所对的边分别为 ,若锐角
,若锐角 满足
满足 ,且
,且 ,
, ,求
,求 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省青岛市高三4月统一质量检测考试理科数学试卷(解析版) 题型:选择题
已知三棱锥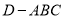 中,
中,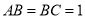 ,
,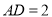 ,
,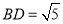 ,
,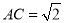 ,
,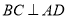 ,则三棱锥的外接球的表面积为( )
,则三棱锥的外接球的表面积为( )
A. B.
B. 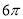 C.
C. 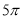 D.
D. 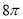
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省青岛市高三4月统一质量检测考试文科数学试卷(解析版) 题型:填空题
已知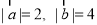 ,
,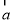 和
和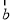 的夹角为
的夹角为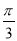 ,以
,以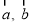 为邻边作平行四边形,则该四边形的面积为 .
为邻边作平行四边形,则该四边形的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com