
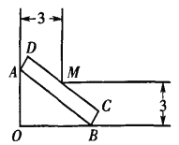
【题目】某建筑物内一个水平直角型过道如图所示.两过道的宽度均为![]() ,有一个水平截面为矩形的设备需要水平移进直角型过道.若该设备水平截面矩形的宽为
,有一个水平截面为矩形的设备需要水平移进直角型过道.若该设备水平截面矩形的宽为![]() ,长为
,长为![]() ,试问:该设备能否水平移进直角型过道?
,试问:该设备能否水平移进直角型过道?
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
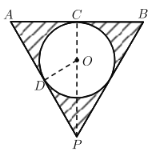
【题目】有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为![]() 的铁球,并注入水,使水面与球正好相切,然后将球取出,则这时容器中水的深度为___________.
的铁球,并注入水,使水面与球正好相切,然后将球取出,则这时容器中水的深度为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.图1是甲套设备的样本的频率分布直方图,表1是乙套设备的样本的频数分布表.
内,则为合格品,否则为不合格品.图1是甲套设备的样本的频率分布直方图,表1是乙套设备的样本的频数分布表.
图1:甲套设备的样本的频率分布直方图

表1:乙套设备的样本的频数分布表
质量指标数 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据上述所得统计数据,计算产品合格率,并对两套设备的优劣进行比较;
(2)填写下面列联表,并根据列联表判断是否有95%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备 | 乙套设备 | 合计 | |
合格 | |||
不合格 | |||
合计 |
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]() 其中
其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着6月6日![]() 商用牌照发放,中国正式进入
商用牌照发放,中国正式进入![]() 商用时代.某人在一山坡
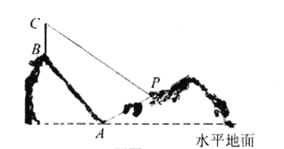
商用时代.某人在一山坡![]() 处观测对面山顶上的一座
处观测对面山顶上的一座![]() 基站(如图),图中所示的山坡均可视为直线,其中基站所在的山坡
基站(如图),图中所示的山坡均可视为直线,其中基站所在的山坡![]() 的坡角为
的坡角为![]() ,点
,点![]() 所在山坡
所在山坡![]() 的坡度为
的坡度为![]() .基站点
.基站点![]() 距坡谷点
距坡谷点![]() 的距离为
的距离为![]() 米,点
米,点![]() 距坡谷点
距坡谷点![]() 的距离为
的距离为![]() 米,且在点
米,且在点![]() 处测得塔顶点
处测得塔顶点![]() 的仰角是
的仰角是![]() .求基站
.求基站![]() 的高度.(参考数据:
的高度.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 个数
个数![]() ,
,![]() ,…,
,…,![]() 的连乘积
的连乘积![]() 记为
记为![]() ,将
,将![]() 个数
个数![]() ,
,![]() ,…,
,…,![]() 的和
的和![]() 记为
记为![]() .(
.(![]() )
)
(1)若数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,求
,求![]() ;
;
(2)用![]() 表示不超过
表示不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() ,
,![]() .若数列
.若数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设定义在正整数集![]() 上的函数
上的函数![]() 满足:当
满足:当![]() (
(![]() )时,
)时,![]() ,问是否存在正整数
,问是否存在正整数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由(已知
的值;若不存在,说明理由(已知![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆![]() 上取一点
上取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线段
轴的垂线段![]() ,
,![]() 为垂足,当点
为垂足,当点![]() 在圆
在圆![]() 上运动时,设线段
上运动时,设线段![]() 中点
中点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)试问在![]() 上是否存在两点
上是否存在两点![]() 关于直线
关于直线![]() 对称,且以
对称,且以![]() 为直径的圆恰好经过坐标原点?若存在,求出直线
为直径的圆恰好经过坐标原点?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲,乙两地某月![]() 时的气温,随机选取该月中的
时的气温,随机选取该月中的![]() 天,将这
天,将这![]() 天中
天中![]() 时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:①甲地该月
时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:①甲地该月![]() 时的平均气温低于乙地该月
时的平均气温低于乙地该月![]() 时的平均气温;②甲地该月
时的平均气温;②甲地该月![]() 时的平均气温高于乙地该月
时的平均气温高于乙地该月![]() 时的平均气温;③甲地该月
时的平均气温;③甲地该月![]() 时的气温的中位数小于乙地该月
时的气温的中位数小于乙地该月![]() 时的气温的中位数;④甲地该月
时的气温的中位数;④甲地该月![]() 时的气温的中位数大于乙地该月
时的气温的中位数大于乙地该月![]() 时的气温的中位数.其中根据茎叶图能得到的正确结论的编号为( )
时的气温的中位数.其中根据茎叶图能得到的正确结论的编号为( )

A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com