
(本小题12分)某公司生产一种产品每年需投入固定成本为0.5万元,此外每生产100件这种产品还需要增加投入0.25万元.经预测知,当售出这种产品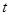 百件时,若
百件时,若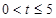 ,则销售所得的收入为
,则销售所得的收入为 万元:若
万元:若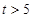 ,则销售收入为
,则销售收入为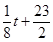 万元.
万元.
(1)若该公司的这种产品的年产量为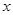 百件
百件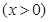 ,请把该公司生产并销售这种产品所得的年利润
,请把该公司生产并销售这种产品所得的年利润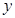 表示为当年生产量
表示为当年生产量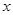 的函数;
的函数;
(2)当年产量为多少时,当年公司所获利润最大?
(1)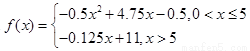
(2)当年产量为4.75(百件)时,当年公司所得利润最大,最大为10.78125万元.
【解析】
试题分析:(1)分类讨论:①当0≤x≤5时,②当x>5时,分别写出函数f(x)的表达式,最后利用分段函数的形式写出所求函数解析式即可;
(2)分别求出当0≤x≤5时,及当x>5时,f(x)的最大值,最后综上所述,当x为多少时,f(x)有最大值,即当年产量为多少件时,公司可获得最大年利润.
解:(1)当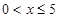 时,
时,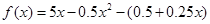 =
=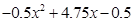
当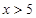 时,
时,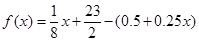

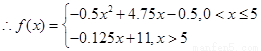
(2)当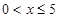 时,
时,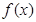 =
=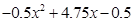 =
=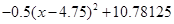
 当
当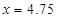 时,
时,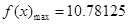
当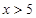 时,
时,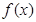

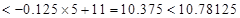
 当年产量为4.75(百件)时,当年公司所得利润最大,最大为10.78125万元.
当年产量为4.75(百件)时,当年公司所得利润最大,最大为10.78125万元.
考点:本题主要考查了分段函数,以及函数与方程的思想,属于基础题..
点评:解决该试题的关键是函数模型为分段函数,求分段函数的最值,应先求出函数在各部分的最值,然后取各部分的最值的最大值为整个函数的最大值,取各部分的最小者为整个函数的最小值。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com