
【题目】已知随机变量 ![]() 的取值为不大于
的取值为不大于 ![]() 的非负整数值,它的分布列为:
的非负整数值,它的分布列为:
| 0 | 1 | 2 |
| n |
|
|
|
|
|
|
其中 ![]() (
( ![]() )满足:
)满足: ![]() ,且
,且 ![]() .
.
定义由 ![]() 生成的函数
生成的函数 ![]() ,令
,令 ![]() .
.
(I)若由 ![]() 生成的函数
生成的函数 ![]() ,求
,求 ![]() 的值;
的值;
(II)求证:随机变量 ![]() 的数学期望
的数学期望 ![]() ,
, ![]() 的方差
的方差 ![]() ;
;
( ![]() )
)
(Ⅲ)现投掷一枚骰子两次,随机变量 ![]() 表示两次掷出的点数之和,此时由
表示两次掷出的点数之和,此时由 ![]() 生成的函数记为
生成的函数记为 ![]() ,求
,求 ![]() 的值.
的值.
【答案】解:(I) ![]() .
.
(II)由于 ![]() ,
,
![]() ,
,
所以 ![]() .
.
由 ![]() 的方差定义可知
的方差定义可知
![]()
![]()
![]()
![]()
![]()
由于 ![]() ,所以有
,所以有
![]() ,这样
,这样
![]() ,所以有
,所以有
![]() .
.
(III)由题意可知 ![]() 的取值为2,3,4,5,6,7,8,9,10,11,12
的取值为2,3,4,5,6,7,8,9,10,11,12
则 ![]() 的分布列为
的分布列为
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
|
|
|
|
|
|
 则
则 ![]()
![]()
【解析】(1)由题意可求出其值。(2)结合题意根据数学期望值得公式即可求出结果。(2)根据题意可知 ξ 的取值由题意可求出各个取值的概率列表求出即可。
【考点精析】利用离散型随机变量及其分布列对题目进行判断即可得到答案,需要熟知在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】【2018海南高三阶段性测试(二模)】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一动点.
上一动点.
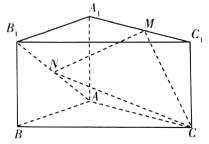
(I)是否存在一点![]() ,使得线段
,使得线段![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
(II)若点![]() 为
为![]() 的中点且
的中点且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举办校园科技文化艺术节,在同一时间安排《生活趣味数学》和《校园舞蹈赏析》两场讲座.已知A、B两学习小组各有5位同学,每位同学在两场讲座任意选听一场.若A组1人选听《生活趣味数学》,其余4人选听《校园舞蹈赏析》;B组2人选听《生活趣味数学》,其余3人选听《校园舞蹈赏析》.
(1)若从此10人中任意选出3人,求选出的3人中恰有2人选听《校园舞蹈赏析》的概率;
(2)若从A、B两组中各任选2人,设X为选出的4人中选听《生活趣味数学》的人数,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,a1=1,前n项和为Sn , 且an+12﹣nλ2﹣1=2λSn , λ为正常数.
(1)求数列{an}的通项公式;
(2)记bn= ![]() ,Cn=
,Cn= ![]() +
+ ![]() (k,n∈N*,k≥2n+2). 求证:
(k,n∈N*,k≥2n+2). 求证:
①bn<bn+1;
②Cn>Cn+1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究函数f(x)= ![]() 的性质,完成下面两个问题:
的性质,完成下面两个问题:
①将f(2),f(3),f(5)按从小到大排列为;
②函数g(x)= ![]() (x> 0)的最大值为 .
(x> 0)的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点. 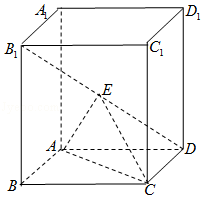
(Ⅰ)证明:平面ACE⊥平面ABCD;
(Ⅱ)若二面角D﹣AE﹣C为60°,AA1=AB=1,求三棱锥C﹣AED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体中, ![]() 菱形,
菱形, ![]() 是矩形,
是矩形, ![]() ⊥平面
⊥平面 ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)异面直线 ![]() 与
与 ![]() 所成的角余弦值;
所成的角余弦值;
(Ⅱ)求证平面 ![]() ⊥平面
⊥平面 ![]() ;
;
(Ⅲ)在线段 ![]() 取一点
取一点 ![]() ,当二面角
,当二面角 ![]() 的大小为60°时,求
的大小为60°时,求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①若![]() ,则
,则![]() ;
;
②已知![]() ,
,![]() ,且
,且![]() 与
与![]() 的夹角为锐角,则实数
的夹角为锐角,则实数![]() 的取值范围是
的取值范围是![]() ;
;
③已知![]() 是平面上一定点,
是平面上一定点,![]() 是平面上不共线的三个点,动点
是平面上不共线的三个点,动点![]() 满足
满足![]() ,
,![]() ,则
,则![]() 的轨迹一定通过
的轨迹一定通过![]() 的重心;
的重心;
④在![]() 中,
中,![]() ,边长
,边长![]() 分别为
分别为![]() ,则
,则![]() 只有一解;
只有一解;
⑤如果△ABC内接于半径为![]() 的圆,且
的圆,且![]()
则△ABC的面积的最大值![]() ;
;
其中正确的序号为_______________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com