
【题目】在△ABC中,设边a,b,c所对的角为A,B,C,且A,B,C都不是直角,(bc﹣8)cosA+accosB=a2﹣b2 . (Ⅰ)若b+c=5,求b,c的值;
(Ⅱ)若 ![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
【答案】解:(Ⅰ)∵ ![]() , ∴
, ∴ ![]() ,
,
∴ ![]() ,
,
∵△ABC不是直角三角形,
∴bc=4,
又∵b+c=5,
∴解得 ![]() 或
或 ![]()
(Ⅱ)∵ ![]() ,由余弦定理可得5=b2+c2﹣2bccosA≥2bc﹣2bccosA=8﹣8cosA,
,由余弦定理可得5=b2+c2﹣2bccosA≥2bc﹣2bccosA=8﹣8cosA,
∴ ![]() ,
,
∴ ![]() ,所以
,所以 ![]() .
.
∴△ABC面积的最大值是 ![]() ,当
,当 ![]() 时取到
时取到
【解析】(Ⅰ)由已知利用余弦定理化简已知等式可得 ![]() ,又△ABC不是直角三角形,解得bc=4,又b+c=5,联立即可解得b,c的值.(Ⅱ)由余弦定理,基本不等式可得5=b2+c2﹣2bccosA≥2bc﹣2bccosA=8﹣8cosA,解得
,又△ABC不是直角三角形,解得bc=4,又b+c=5,联立即可解得b,c的值.(Ⅱ)由余弦定理,基本不等式可得5=b2+c2﹣2bccosA≥2bc﹣2bccosA=8﹣8cosA,解得 ![]() ,可求
,可求 ![]() ,利用三角形面积公式即可得解三角形面积的最大值.
,利用三角形面积公式即可得解三角形面积的最大值.
【考点精析】掌握正弦定理的定义和余弦定理的定义是解答本题的根本,需要知道正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】(2015·湖北)设函数![]() ,
,![]() 的定义域均为
的定义域均为![]() ,且
,且![]() 是奇函数,
是奇函数,![]() 是偶函数,
是偶函数,![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(Ⅰ)求![]() ,
,![]() 的解析式,并证明:当
的解析式,并证明:当![]() 时,
时,![]() ,
,![]() ;
;
(Ⅱ)设![]() ,
,![]() ,证明:当
,证明:当![]() 时,
时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
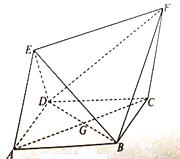
【题目】如图,四边形 ![]() 为菱形,四边形
为菱形,四边形 ![]() 为平行四边形,设
为平行四边形,设 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,
, ![]() .
.
(1)证明:平面 ![]() 平面
平面 ![]() ;
;
(2)若 ![]() 与平面
与平面 ![]() 所成角为60°,求二面角
所成角为60°,求二面角 ![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( ) (1.)已知等比数列{an},则“数列{an}单调递增”是“数列{an}的公比q>1”的充分不必要条件;
(2.)二项式 ![]() 的展开式按一定次序排列,则无理项互不相邻的概率是
的展开式按一定次序排列,则无理项互不相邻的概率是 ![]() ;
;
(3.)已知 ![]() ,则
,则 ![]() ;
;
(4.)为了解1000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为40.
A.(1)(2)
B.(2)(3)
C.(1)(3)
D.(2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,以x轴的正半轴为极轴建立极坐标系.设曲线C的参数方程为 ![]() (α是参数),直线l的极坐标方程为ρcos(θ+
(α是参数),直线l的极坐标方程为ρcos(θ+ ![]() )=2
)=2 ![]() .
.
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)设点P为曲线C上任意一点,求点P到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了了解老人们的健康状况,政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行统计,样本分布被制作成如图表: 
(1)若采用分层抽样的方法再从样本中的不能自理的老人中抽取8人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发放生活补贴,标准如下: ①80岁及以上长者每人每月发放生活补贴200元;
②80岁以下老人每人每月发放生活补贴120元;
③不能自理的老人每人每月额外发放生活补贴100元.试估计政府执行此计划的年度预算.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的最小正周期为4π,则( )
的最小正周期为4π,则( )
A.函数f(x)的图象关于原点对称
B.函数f(x)的图象关于直线 ![]() 对称
对称
C.函数f(x)图象上的所有点向右平移 ![]() 个单位长度后,所得的图象关于原点对称
个单位长度后,所得的图象关于原点对称
D.函数f(x)在区间(0,π)上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣1)lnx﹣(x﹣a)2(a∈R). (Ⅰ)若f(x)在(0,+∞)上单调递减,求a的取值范围;
(Ⅱ)若f(x)有两个极值点x1 , x2 , 求证:x1+x2> ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com