
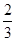 ,乙获胜的概率为
,乙获胜的概率为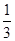 ,假定各次比赛相互独立,比赛经ξ次结束,求:
,假定各次比赛相互独立,比赛经ξ次结束,求: 习题精选系列答案
习题精选系列答案科目:高中数学 来源:不详 题型:解答题
 两个代表队进行乒乓球对抗赛,每队三名队员,
两个代表队进行乒乓球对抗赛,每队三名队员, 队队员是
队队员是  ,
, 队队员是
队队员是 ,按以往多次比赛的统计,对阵队员之间的胜负概率如下:
,按以往多次比赛的统计,对阵队员之间的胜负概率如下:| 对阵队员 |  队队员胜的概率 队队员胜的概率 |  队队员负的概率 队队员负的概率 |
 对 对 |  |  |
 对 对 |  |  |
 对 对 |  |  |
 .
. 的概率分布列;
的概率分布列; ,
, .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从口袋中随机取出一个球是红球的概率是
个白球.已知从口袋中随机取出一个球是红球的概率是 .
.  时,不放回地从口袋中随机取出3个球,求取到白球的个数
时,不放回地从口袋中随机取出3个球,求取到白球的个数 的期望
的期望 ;
; ,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于 ,求
,求 和
和 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。 ,求
,求 的分布列与数学期望。
的分布列与数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
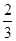 和
和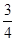 ,且各株大树是否成活互不影响.
,且各株大树是否成活互不影响. ,求
,求 分布列与期望.
分布列与期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
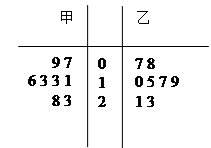
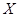 的分布列和均值.(8分)
的分布列和均值.(8分)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| X1 | 5 | 6 | 7 | 8 | 9 | 10 |
| P | 0.03 | 0.09 | 0.20 | 0.31 | 0.27 | 0.10 |
| X2 | 5 | 6 | 7 | 8 | 9 |
| P | 0.01 | 0.05 | 0.20 | 0.41 | 0.33 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com