
【题目】设函数![]() ,
,![]() 是函数
是函数![]() 的导数.
的导数.
(1)若![]() ,证明
,证明![]() 在区间
在区间![]() 上没有零点;
上没有零点;
(2)在![]() 上
上![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析(2)![]()
【解析】
(1)先利用导数的四则运算法则和导数公式求出![]() ,再由函数
,再由函数![]() 的导数可知,
的导数可知,
函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,而
上单调递减,而![]() ,
,![]() ,可知
,可知![]() 在区间
在区间![]() 上恒成立,即
上恒成立,即![]() 在区间
在区间![]() 上没有零点;
上没有零点;
(2)由题意可将![]() 转化为
转化为![]() ,构造函数
,构造函数![]() ,
,
利用导数讨论研究其在![]() 上的单调性,由
上的单调性,由![]() ,即可求出
,即可求出![]() 的取值范围.
的取值范围.
(1)若![]() ,则
,则![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,故函数
,故函数![]() 是奇函数.
是奇函数.
当![]() 时,
时,![]() ,
,![]() ,这时
,这时![]() ,
,
又函数![]() 是奇函数,所以当
是奇函数,所以当![]() 时,
时,![]() .
.
综上,当![]() 时,函数
时,函数![]() 单调递增;当
单调递增;当![]() 时,函数
时,函数![]() 单调递减.
单调递减.
又![]() ,
,![]() ,
,
故![]() 在区间
在区间![]() 上恒成立,所以
上恒成立,所以![]() 在区间
在区间![]() 上没有零点.
上没有零点.
(2)![]() ,由
,由![]() ,所以
,所以![]() 恒成立,
恒成立,
若![]() ,则
,则![]() ,设
,设![]() ,
,
![]()
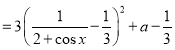 .
.
故当![]() 时,
时,![]() ,又
,又![]() ,所以当
,所以当![]() 时,
时,![]() ,满足题意;
,满足题意;
当![]() 时,有
时,有![]() ,与条件矛盾,舍去;
,与条件矛盾,舍去;
当![]() 时,令
时,令![]() ,则
,则![]() ,
,
又![]() ,故
,故![]() 在区间
在区间![]() 上有无穷多个零点,
上有无穷多个零点,
设最小的零点为![]() ,
,
则当![]() 时,
时,![]() ,因此
,因此![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,所以
,所以![]() .
.
于是,当![]() 时,
时,![]() ,得
,得![]() ,与条件矛盾.
,与条件矛盾.
故![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并与圆
外切并与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,问是否在
两点,问是否在![]() 轴上存在一点
轴上存在一点![]() ,使得当
,使得当![]() 变动时总有
变动时总有![]() ?若存在,请说明理由.
?若存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 上一点,点
上一点,点![]() 为抛物线
为抛物线![]() 的焦点,
的焦点,![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 的另一个交点为
的另一个交点为![]() ,曲线
,曲线![]() 在点
在点![]() 与点
与点![]() 处的切线分别为
处的切线分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县为了帮助农户脱贫致富,鼓励农户利用荒地山坡种植果树,某农户考察了三种不同的果树苗![]() 、
、![]() 、
、![]() .经过引种实验发现,引种树苗
.经过引种实验发现,引种树苗![]() 的自然成活率为
的自然成活率为![]() ,引种树苗
,引种树苗![]() 、
、![]() 的自然成活率均为
的自然成活率均为![]() .
.
(1)任取树苗![]() 、
、![]() 、
、![]() 各一棵,估计自然成活的棵数为
各一棵,估计自然成活的棵数为![]() ,求
,求![]() 的分布列及其数学期望;
的分布列及其数学期望;
(2)将(1)中的数学期望取得最大值时![]() 的值作为
的值作为![]() 种树苗自然成活的概率.该农户决定引种
种树苗自然成活的概率.该农户决定引种![]() 棵
棵![]() 种树苗,引种后没有自然成活的树苗有
种树苗,引种后没有自然成活的树苗有![]() 的树苗可经过人工栽培技术处理,处理后成活的概率为
的树苗可经过人工栽培技术处理,处理后成活的概率为![]() ,其余的树苗不能成活.
,其余的树苗不能成活.
①求一棵![]() 种树苗最终成活的概率;
种树苗最终成活的概率;
②若每棵树苗引种最终成活可获利![]() 元,不成活的每棵亏损
元,不成活的每棵亏损![]() 元,该农户为了获利期望不低于
元,该农户为了获利期望不低于![]() 万元,问至少要引种
万元,问至少要引种![]() 种树苗多少棵?
种树苗多少棵?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 分别为
分别为![]() 的中点,设直线
的中点,设直线![]() 与平面
与平面![]() 交于点
交于点![]() .
.

(1)已知平面![]() 平面
平面![]() ,求证:
,求证: ![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着时代的发展和社会的进步,“农村淘宝”发展十分迅速,促进“农产品进城”和“消费品下乡”,“农产品进城”很好地解决了农产品与市场的对接问题,使农民收入逐步提高,生活水平得到改善,农村从事网店经营的人收入逐步提高.西凤脐橙是四川省南充市的特产,因果实呈椭圆形、色泽橙红、果面光滑、无核、果肉脆嫩化渣、汁多味浓,深受人们的喜爱.为此小王开网店销售西凤脐橙,每月月初购进西凤脐橙,每售出1吨西凤脐橙获利润800元,未售出的西凤脐橙,每1吨亏损500元.经市场调研,根据以往的销售统计,得到一个月内西凤脐橙市场的需求量的频率分布直方图如图所示.小王为下一个月购进了100吨西凤脐橙,以x(单位:吨)表示下一个月内市场的需求量,y(单位:元)表示下一个月内经销西凤脐橙的销售利润.
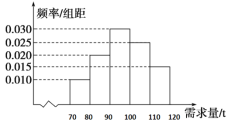
(1)将y表示为x的函数;
(2)根据频率分布直方图估计小王的网店下一个月销售利润y不少于67000元的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 与曲线
与曲线![]() 公共点的极坐标;
公共点的极坐标;
(2)设过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com