
【题目】以下关于圆锥曲线的命题中:①双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点;②设
有相同的焦点;②设![]() 、
、![]() 是两个定点,
是两个定点,![]() 为非零常数,若
为非零常数,若![]() ,则动点
,则动点![]() 的轨迹为双曲线的一支;③设点
的轨迹为双曲线的一支;③设点![]() 、
、![]() 分别是定圆
分别是定圆![]() 上一个定点和动点,
上一个定点和动点,![]() 为坐标原点,若
为坐标原点,若![]() ,则动点
,则动点![]() 的轨迹为圆;其中真命题是_________.(写出所有真命题的序号)
的轨迹为圆;其中真命题是_________.(写出所有真命题的序号)
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶7元,未售出的酸奶降价处理,以每瓶1.5元的价格当天全部处理完.据往年销售经验,每天需求量与当天最高气温(单位:![]() )有关,如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
)有关,如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得到下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得到下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 14 | 34 | 27 | 9 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元),若该超市在六月份每天的进货量均为450瓶,写出
(单位:元),若该超市在六月份每天的进货量均为450瓶,写出![]() 的所有可能值,并估计
的所有可能值,并估计![]() 大于零的概率.
大于零的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2019的自主招生考试中,考生笔试成绩分布在![]() ,随机抽取200名考生成绩作为样本研究,按照笔试成绩分成5组,第1组成绩为
,随机抽取200名考生成绩作为样本研究,按照笔试成绩分成5组,第1组成绩为![]() ,第2组成绩为
,第2组成绩为![]() ,第3组成绩为
,第3组成绩为![]() ,第4组成绩为
,第4组成绩为![]() ,第5组成绩为
,第5组成绩为![]() ,样本频率分布直方图如下:
,样本频率分布直方图如下:
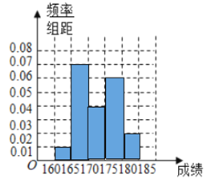
(1)估计全体考生成绩的中位数;
(2)为了能选拨出最优秀的学生,该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,从这6名学生中随机抽取2名学生进行外语交流面试,求这2名学生均来自同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂每年定期对职工进行培训以提高工人的生产能力(生产能力是指一天加工的零件数).现有![]() 、
、![]() 两类培训,为了比较哪类培训更有利于提高工人的生产能力,工厂决定从同一车间随机抽取100名工人平均分成两个小组分别参加这两类培训.培训后测试各组工人的生产能力得到如下频率分布直方图.
两类培训,为了比较哪类培训更有利于提高工人的生产能力,工厂决定从同一车间随机抽取100名工人平均分成两个小组分别参加这两类培训.培训后测试各组工人的生产能力得到如下频率分布直方图.
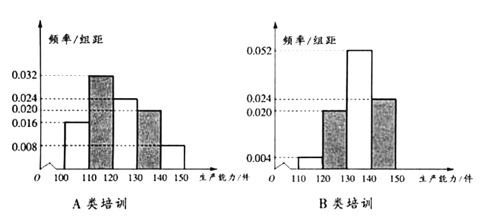
(1)记![]() 表示事件“参加
表示事件“参加![]() 类培训工人的生产能力不低于130件”,估计事件
类培训工人的生产能力不低于130件”,估计事件![]() 的概率;
的概率;
(2)填写下面列联表,并根据列联表判断是否有![]() 的把握认为工人的生产能力与培训类有关:
的把握认为工人的生产能力与培训类有关:
生产能力 | 生产能力 | 总计 | |
| 50 | ||
| 50 | ||
总计 | 100 |
(3)根据频率分布直方图,判断哪类培训更有利于提高工人的生产能力,请说明理由.
参考数据
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() .
.
(1)若椭圆![]() 的离心率为
的离心率为![]() ,求
,求![]() 的值;
的值;
(2)若过点![]() 任作一条直线
任作一条直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() , 若存在,求出点
, 若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图一是美丽的“勾股树”,它是一个直角三角形分别以它的每一边向外作正方形而得到.图二是第1代“勾股树”,重复图二的作法,得到图三为第2代“勾股树”,以此类推,已知最大的正方形面积为1,则第![]() 代“勾股树”所有正方形的个数与面积的和分别为( )
代“勾股树”所有正方形的个数与面积的和分别为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com