
【题目】如图,已知三棱柱![]() 的侧棱与底面垂直,
的侧棱与底面垂直,![]() ,
,![]() ,M是
,M是![]() 的中点,
的中点,![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上,且满足
上,且满足![]() .
.
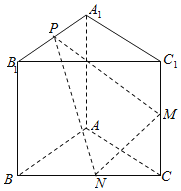
(1)证明:![]() .
.
(2)当![]() 取何值时,直线
取何值时,直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 最大?并求该角最大值的正切值.
最大?并求该角最大值的正切值.
(3)若平面![]() 与平面
与平面![]() 所成的二面角为
所成的二面角为![]() ,试确定P点的位置.
,试确定P点的位置.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)以AB,AC,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,求出各点的坐标及对应向量的坐标,易判断
,求出各点的坐标及对应向量的坐标,易判断![]() ,即
,即![]() ;(2)设出平面ABC的一个法向量,我们易表达出
;(2)设出平面ABC的一个法向量,我们易表达出![]() ,然后利用正弦函数的单调性及正切函数的单调性的关系,求出满足条件的
,然后利用正弦函数的单调性及正切函数的单调性的关系,求出满足条件的![]() 值,进而求出此时
值,进而求出此时![]() 的正线值;(3)平面PMN与平面ABC所成的二面角为
的正线值;(3)平面PMN与平面ABC所成的二面角为![]() ,则平面PMN与平面ABC法向量的夹角余弦值的绝对值为
,则平面PMN与平面ABC法向量的夹角余弦值的绝对值为![]() ,代入向量夹角公式,可以构造一个关于
,代入向量夹角公式,可以构造一个关于![]() 的方程,解方程即可求出对应
的方程,解方程即可求出对应![]() 值,进而确定出满足条件的点P的位置.
值,进而确定出满足条件的点P的位置.
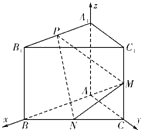
(1)证明:如图,以AB,AC,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,
从而![]() ,
,![]() ,
,
![]() ,
,
所以![]() .
.
(2)平面ABC的一个法向量为![]() ,
,
则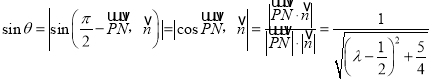 (※).
(※).
而![]() ,当
,当![]() 最大时,
最大时,![]() 最大,
最大,![]() 无意义,
无意义,![]() 除外,
除外,
由(※)式,当![]() 时,
时,![]() ,
,![]() .
.
(3)平面ABC的一个法向量为![]() .
.
设平面PMN的一个法向量为![]() ,
,
由(1)得![]() .
.
由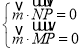 得
得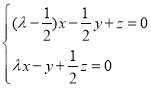 ,
,
解得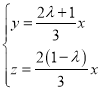 ,令
,令![]() ,得
,得![]() ,
,
∵平面PMN与平面ABC所成的二面角为![]() ,
,
∴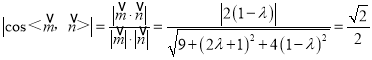 ,
,
解得![]() .
.
故点P在![]() 的延长线上,且
的延长线上,且![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的长轴长为4,焦距为
的长轴长为4,焦距为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过动点![]() 的直线交
的直线交![]() 轴与点
轴与点![]() ,交
,交![]() 于点
于点![]() (
(![]() 在第一象限),且
在第一象限),且![]() 是线段
是线段![]() 的中点.过点
的中点.过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于另一点
于另一点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
(ⅰ)设直线![]() 的斜率分别为
的斜率分别为![]() ,证明
,证明![]() 为定值;
为定值;
(ⅱ)求直线![]() 的斜率的最小值.
的斜率的最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果你留心使会发现,汽车前灯后的反射镜呈抛物线的形状,把抛物线沿它的对称轴旋转一周,就会形成一个抛物面.这种抛物面形状,正是我们熟悉的汽车前灯的反射镜形状,这种形状使车灯既能够发出明亮的、照射很远的平行光束,又能发出较暗的,照射近距离的光线.我们都知道常规的前照灯主要是由灯泡、反射镜和透镜三部分组成,明亮的光束,是由位于抛物面形状反射镜焦点的光源射出的,灯泡位于抛物面的焦点上,灯泡发出的光经抛物面反射镜反射形成平行光束,再经过配光镜的散射、偏转作用,以达到照亮路面的效果,这样的灯光我们通常称为远光灯:而较暗的光线,不是由反射镜焦点的光源射出的,光线的行进与抛物线的对称轴不平行,光线只能向上和向下照射,所以照射距离并不远,如果把向上射出的光线遮住.车灯就只能发出向下的、射的很近的光线了.请用数学的语言归纳表达远光灯的照明原理,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了选拔学生参加全市中学生物理竞赛,学校先从高三年级选取60名同学进行竞赛预选赛,将参加预选赛的学生成绩(单位:分)按范围![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图如图:
分组,得到的频率分布直方图如图:

(1)计算这次预选赛的平均成绩(同一组中的数据用该组区间的中点值作代表);
(2)若对得分在前![]() 的学生进行校内奖励,估计获奖分数线;
的学生进行校内奖励,估计获奖分数线;
(3)若这60名学生中男女生比例为![]() ,成绩不低于60分评估为“成绩良好”,否则评估为“成绩一般”,试完成下面
,成绩不低于60分评估为“成绩良好”,否则评估为“成绩一般”,试完成下面![]() 列联表,是否有
列联表,是否有![]() 的把握认为“成绩良好”与“性别”有关?
的把握认为“成绩良好”与“性别”有关?
成绩良好 | 成绩一般 | 合计 | |
男生 | |||
女生 | |||
合计 |
附:![]() ,
,![]()
临界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,圆
,圆![]() :
:![]() .
.
(1)若过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 方程;
方程;
(2)在(1)的条件下,若直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,
两点,![]() 轴上是否存在点
轴上是否存在点![]() 使
使![]() (
(![]() 为坐标原点)?若存在,求出点
为坐标原点)?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》中记载了有关特殊几何体的定义:阳马指底面为矩形,一侧棱垂直于底面的四棱锥,堑堵指底面是直角三角形,且侧棱垂直于底面的三棱柱.
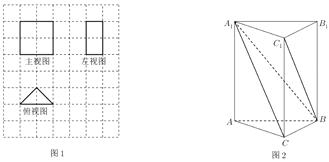
(1)某堑堵的三视图,如图1,网格中的每个小正方形的边长为1,求该堑堵的体积;
(2)在堑堵![]() 中,如图2,
中,如图2,![]() ,若
,若![]() ,当阳马
,当阳马![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充,已知金字塔的每一条棱和边都相等.
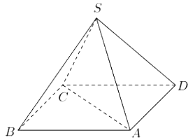
(1)求证:直线AC垂直于直线SD;
(2)若搭边框共使用木料24米,则需要多少立方米的填充材料才能将整个金字塔内部填满?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的各项都不为零,其前n项和为
的各项都不为零,其前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 满足
满足![]() ,其中t为正整数.
,其中t为正整数.
![]() 求
求![]() ;
;
![]() 若不等式
若不等式![]() 对任意
对任意![]() 都成立,求首项
都成立,求首项![]() 的取值范围;
的取值范围;
![]() 若首项
若首项![]() 是正整数,则数列
是正整数,则数列![]() 中的任意一项是否总可以表示为数列
中的任意一项是否总可以表示为数列![]() 中的其他两项之积?若是,请给出一种表示方式;若不是,请说明理由.
中的其他两项之积?若是,请给出一种表示方式;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com