练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

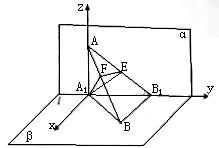
    如图在二面角α- l-β中，A、B∈α，C、D∈l，ABCD为矩形，P∈β，PA⊥α，且PA=AD，MN依次是AB、PC的中点

    ⑴ 求二面角α- l-β的大小

    ⑵ 求证明：MN⊥AB

    ⑶ 求异面直线PA与MN所成角的大小


    解析:

    ⑴ 用垂线法作二面角的平面角

    ⑵ 只要证明AB垂直于过MN的一个平面即可

    ⑶ 过点A作MN的平行线，转化为平面角求解

    解：

    ⑴ 连PD

        ∵PA⊥α，AD⊥l

        ∴PD⊥l

        ∴∠PDA为二面角α- l-β的平面角

        在RTΔPAD中

        ∵PA=PD

        ∴∠PDA=45°

        ∴二面角α- l-β为45°

    ⑵ 设E是DC的中点，连ME、NE

    ∵M、N、E分别为AB、PC、D的中点

    ∴ME∥AD，NE∥PD

    ∴ME⊥l，NE⊥l

    ∴l⊥平面MEN

    ∵AB∥l

    ∴AB⊥平面MEN

    ∵MN??平面MNE

    ∴MN^AB

    ⑶ 设Q是DP听中点，连NQ、AQ

       则NQ∥DC，且NQ=1/2DC

       ∵AM∥DC，且AM=1/2AB=1/2DC

       ∴QN∥AM，QN=AM

       ∴QNMQ为平行四边形

       ∴AQ∥MN

       ∴∠PAQ为PA与MN所成的角

       ∵ΔPAQ为等腰直角三角形，AQ为斜边上的中线

       ∴∠PAQ=45°

       即PA与MN所成角的大小为45°

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，在二面角M-l-N的一个M内有Rt△ABC，其中∠A=90°，顶点B、C在二面角的棱l上，AB、AC与平面N所成的角分别为α、β，若二面角M-l-N的大小为θ，则下面的关系式中正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源：湖北省荆州中学2008高考复习立体几何基础题题库一(有详细答案)人教版 人教版 题型：044

    如图在二面角α－l－β中，A、B∈α，C、D∈l，ABCD为矩形，P∈β，PA⊥α，且PA＝AD，MN依次是AB、PC的中点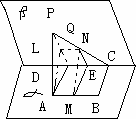

    (1)求二面角α－l－β的大小

    (2)求证明：MN⊥AB

    (3)求异面直线PA与MN所成角的大小

    查看答案和解析>>

    科目：高中数学 来源： 题型：

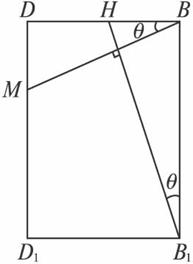
    (理)如图,在四棱锥P—ABCD中,侧面PAD是正三角形且与底面ABCD垂直,底面ABCD是矩形,E是AB的中点,PC与平面ABCD所成的角为30°.

    (1)若平面PAB∩平面PCD=l,试判断直线l与平面ABCD的关系,并加以证明;

    (2)求平面PAB与平面PCD所成二面角的大小;

    (3)当AD为多长时,点D到平面PCE的距离为2?

    (文)在正四棱柱ABCD—A1B1C1D1中,BB1=2AB=4,E、F分别是棱AB与BC的中点.

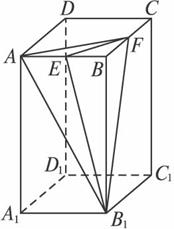
    (1)求二面角EFB1B的平面角的正切值.

    (2)在棱DD1上能否找到一点M,使BM⊥平面B1EF?若能,试确定M的位置;若不能,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    19.

    如图，α⊥β，α∩β＝l，A∈α，B∈β，点A在直线l上的射影为A1，点B在直线l上的射影为B1，已知AB＝2，AA1=1，BB1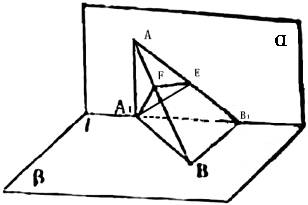＝Equation.3，求：

    （Ⅰ）直线AB分别与平面α，β所成的角的大小；

    （Ⅱ）二面角A1－AB－B1的大小.

    查看答案和解析>>

    同步练习册答案