
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且点
,且点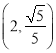 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,在直线
两点,在直线![]() 上存在点
上存在点![]() ,使三角形
,使三角形![]() 为正三角形,求
为正三角形,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由离心率得![]() ,再把已知点的坐标代入椭圆方程,结合
,再把已知点的坐标代入椭圆方程,结合![]() 可解得
可解得![]() ,得椭圆方程;
,得椭圆方程;
(2)设直线![]() 方程为
方程为![]() ,与
,与![]() 联立方程组,消去
联立方程组,消去![]() ,设
,设![]() ,
,![]() ,由韦达定理得
,由韦达定理得![]()
![]() .设线段
.设线段![]() 的中点为
的中点为![]() ,得直线
,得直线![]() 方程,求出
方程,求出![]() 点坐标(此结论对
点坐标(此结论对![]() 也适用),
也适用),![]() 是等边三角形等价于
是等边三角形等价于![]() ,由此可把
,由此可把![]() 用
用![]() 表示,设
表示,设![]() 换元后,可利用基本不等式求得最值.
换元后,可利用基本不等式求得最值.
(1)设![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
由点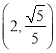 在椭圆
在椭圆![]() 上得
上得![]() ,
,
![]() ,
,![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .
.
(2)显然,直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]() ,
,
与![]() 联立方程组,消去
联立方程组,消去![]() ,并化简得
,并化简得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
设线段![]() 的中点为
的中点为![]() ,则直线
,则直线![]() :
:![]() ,令
,令![]() ,
,
又![]() ,得点
,得点![]() 的坐标为
的坐标为![]() ,显然当
,显然当![]() 时也符合,
时也符合,
所以![]() .
.
又因为![]() ,
,
由三角形![]() 为正三角形得
为正三角形得![]() ,
,
所以![]() 两边平方可得
两边平方可得
 ,得
,得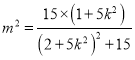 .
.
令![]() ,则
,则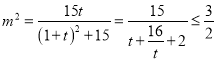 ,当且仅当
,当且仅当![]() ,即
,即![]() 时等号成立,此时
时等号成立,此时![]() ,所以
,所以![]() 的最大值为
的最大值为![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】已知如图一![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 在
在![]() 上,且
上,且![]() ,
,![]() 为
为![]() 中点,将
中点,将![]() 沿
沿![]() 折起,
折起,![]() 沿
沿![]() 折起,使得
折起,使得![]() ,
,![]() 重合于一点(如图二),设为
重合于一点(如图二),设为![]() .
.
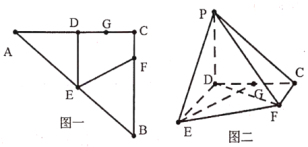
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学一班级1999级同学举行20周年聚会,该班共来了12位同学,其中女同学6位,聚会过程中有一个游戏环节,在游戏环节中,需要随机从中选出2位同学代表,进行男女搭配完成该项游戏,因此,每次选出的2位同学是一男一女,才算“有效选择”;否则视为“无效选择”,继续下一次选择,直到成为“有效选择”为止.
(1)求第一次随机选出的2位同学是“有效选择”的概率;
(2)设第一次选出的2位同学代表中女同学人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了有效地加强高中生自主管理能力,推出了一系列措施,其中自习课时间的自主管理作为重点项目,学校有关处室制定了“高中生自习课时间自主管理方案”.现准备对该“方案”进行调查,并根据调查结果决定是否启用该“方案”,调查人员分别在各个年级随机抽取若干学生对该“方案”进行评分,并将评分分成![]() ,
,![]() ,
,![]() ,
,![]() 七组,绘制成如图所示的频率分布直方图.
七组,绘制成如图所示的频率分布直方图.
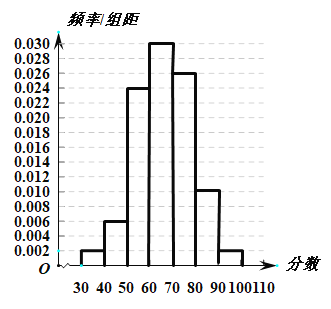
相关规则为①采用百分制评分,![]() 内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于
内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于![]() 即可启用该“方案”;③用样本的频率代替概率.
即可启用该“方案”;③用样本的频率代替概率.
(1)从该校学生中随机抽取1人,求被抽取的这位同学非常满意该“方案”的概率,并根据频率分布直方图求学生对该“方案”评分的中位数.
(2)根据所学统计知识,判断该校是否启用该“方案”,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,共享单车在我国各城市迅猛发展,为人们的出行提供了便利,但也给城市的交通管理带来了一些困难,为掌握共享单车在![]() 省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的
省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的![]() 指标
指标![]() 和
和![]() 指标
指标![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并说明
,并说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则认为
,则认为![]() 与
与![]() 具有较强的线性相关关系,否则认为没有较强的线性相关关系).
具有较强的线性相关关系,否则认为没有较强的线性相关关系).
(2)建立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标为7时,
指标为7时,![]() 指标的估计值.
指标的估计值.
(3)若某城市的共享单车![]() 指标
指标![]() 在区间
在区间![]() 的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至
的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至![]() 指标
指标![]() 在区间
在区间![]() 内现已知
内现已知![]() 省某城市共享单车的
省某城市共享单车的![]() 指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
参考公式:回归直线![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为
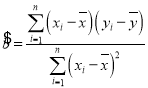 ,,
,,![]() 相关系数
相关系数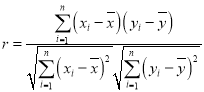
参考数据: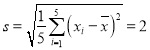 ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com