练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知无穷等比数列{an}的前n项和Sn的极限存在，且a3=4，S5-S2=7，则数列{an}各项的和为________．

    32
    分析：由无穷等比数列{an}的前n项和Sn的极限存在可得，|q|＜1由已知a3=4，S5-S2=7，可得a4+a5=3，利用首项及公比分别表示已知，通过解方程可求a1，q，然后代入数列的各项和公式S=可求
    解答：由无穷等比数列{an}的前n项和Sn的极限存在可得，|q|＜1
    ∵a3=4，7=s5-s2=a3+a4+a5
    ∴a4+a5=a1q3+a1q4=3①a1q2=4，②
    ①②联立可得，，
    ∴
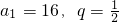
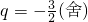
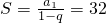
    故答案为：32
    点评：本题主要考查了等比数列的基本运算，利用a1，q表示等比数列的项及和，而熟练掌握基本概念、基本运算是解决本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    10、已知无穷等比数列{an}的前n项的积为Tn，且a1＞1，a2008a2009＞1，（a2008-1）（a2009-1）＜0，则这个数列中使Tn＞1成立的最大正整数n的值等于（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知无穷等比数列{an}的前n项和Sn=
    1
    3n
    +a    （n∈N*），且a是常数，则此无穷等比数列各项的和是（　　）
    A、
    1
    3
    B、-
    1
    3
    C、1
    D、-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知无穷等比数列{an}的前n项和Sn=
    13n
    +a(n∈N*)    ，且a是常数，则此无穷等比数列各项的和等于
     
    （用数值作答）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•上海模拟）已知无穷等比数列{an}的前n项和为Sn，各项的和为S，且
    lim
    n→∞
    (Sn-2S)=1    ，则其首项a1的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知无穷等比数列{an}的公比q≠-1,前n项和为Sn,若集合P={x|x= },则集合P的子集个数为(    )

    A.3            B.4              C.7             D.8

    查看答案和解析>>

    同步练习册答案