
【题目】已知函数![]() .
.
(Ⅰ)设曲线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,求曲线在该点处的切线方程;
,求曲线在该点处的切线方程;
(Ⅱ)设方程![]() 有两个实数根
有两个实数根![]() ,
,![]() ,求证:
,求证:![]()
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(Ⅰ)首先求出函数与![]() 轴正半轴交于点
轴正半轴交于点![]() ,求出函数的导函数即可得到
,求出函数的导函数即可得到![]() 即切线的斜率,最后利用点斜式求切线方程;
即切线的斜率,最后利用点斜式求切线方程;
(Ⅱ)求出函数的单调区间,不妨设![]() ,则
,则![]() .首先证明:当
.首先证明:当![]() 时,
时,![]() ,要证
,要证![]() ,只要证
,只要证![]() ,即证
,即证![]() .又
.又![]() ,只要证
,只要证![]() ,即证
,即证![]() .令
.令![]()
利用导数研究函数的单调性从而得到![]() ,即可得证;
,即可得证;
解:(Ⅰ)由![]() ,得
,得![]() .∴
.∴![]() ,即函数与
,即函数与![]() 轴正半轴交于点
轴正半轴交于点![]() ,
,
又因为![]() .
.
∴![]() .
.![]() ,
,
∴曲线在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅱ)令![]() 得
得![]() 或
或![]() .
.
且当![]() 或
或![]() 时
时![]() ;当
;当![]() 时,
时,![]() .
.
∴![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,![]() .
.
当![]() 或
或![]() 时
时![]() ;当
;当![]() 时,
时,![]() .
.
不妨设![]() ,则
,则![]() .
.
下面证明:当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() .
.
易知![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,即当
,即当![]() 时,
时,![]() .
.
由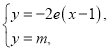 得
得![]() .
.
记![]() .
.
则![]() .
.
要证![]() ,
,
只要证![]() ,即证
,即证![]() .
.
又∵![]() ,∴只要证
,∴只要证![]() ,即证
,即证![]() .
.
∵![]() ,即证
,即证![]() .
.
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() .
.![]() 为单调递减函数;
为单调递减函数;
当![]() 时,
时,![]() .
.![]() 为单调递增函数.
为单调递增函数.
∴![]() ,∴
,∴![]() .
.
∴![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|2x﹣2|的最大值为M,正实数a,b满足a+b=M.
(1)求2a2+b2的最小值;
(2)求证:aabb≥ab.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() :
:![]() (α为参数)经过伸缩变换
(α为参数)经过伸缩变换![]() 得到曲线
得到曲线![]() ,在以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为
,在以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)设点P是曲线![]() 上的动点,求点P到直线l距离d的最大值.
上的动点,求点P到直线l距离d的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在极坐标系![]() 中,
中,![]() ,
,![]() ,弧
,弧![]() ,
,![]() ,
,![]() 所在圆的圆心分别为
所在圆的圆心分别为![]() ,
,![]() ,
,![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() .
.
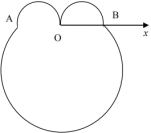
(1)写出曲线![]() ,
,![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)曲线![]() 由
由![]() ,
,![]() ,
,![]() 构成,若曲线
构成,若曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() ),写出曲线
),写出曲线![]() 与曲线
与曲线![]() 的所有公共点(除极点外)的极坐标.
的所有公共点(除极点外)的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三男生体育课上做投篮球游戏,两人一组,每轮游戏中,每小组两人每人投篮两次,投篮投进的次数之和不少于![]() 次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为
次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为![]() .
.
(1)若![]() ,
,![]() ,则在第一轮游戏他们获“优秀小组”的概率;
,则在第一轮游戏他们获“优秀小组”的概率;
(2)若![]() 则游戏中小明小亮小组要想获得“优秀小组”次数为
则游戏中小明小亮小组要想获得“优秀小组”次数为![]() 次,则理论上至少要进行多少轮游戏才行?并求此时
次,则理论上至少要进行多少轮游戏才行?并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月25日-27日,北京召开第二届“一带一路”国际高峰论坛,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为 ( )
A. 198B. 268C. 306D. 378
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com