
【题目】某公司为了获得更大的收益,每年要投入一定的资金用于广告促销,经调查,每年投入广告费t百万元,可增加销售额约为![]() 百万元.
百万元.
(Ⅰ)若该公司将一年的广告费控制在4百万元之内,则应投入多少广告费,才能使该公司由此增加的收益最大?
(Ⅱ)现该公司准备共投入5百万元,分别用于广告促销和技术改造,经预测,每投入技术改造费![]() 百万元,可增加的销售额约为
百万元,可增加的销售额约为![]() 百万元,请设计一个资金分配方案,使该公司由此增加的收益最大.
百万元,请设计一个资金分配方案,使该公司由此增加的收益最大.
(注:收益=销售额-投入,这里除了广告费和技术改造费,不考虑其他的投入)
【答案】(1)投入3百万元的广告费时,该公司由此增加的收益最大.(2)4百万元用于技术改造,1百万元用于广告促销,该公司由此增加的收益最大
【解析】分析:(Ⅰ)先写出收益f(t)的解析式,再利用二次函数的图像和性质求最大值和此时t 的值. (Ⅱ)设由此增加的收益是g(x)百万元,再写出g(x)的解析式,再利用导数求函数的最值,即得资金分配方案.
详解:(Ⅰ)设投入t百万元的广告费后增加的收益为f(t)百万元,
则由![]() ,
,
∴当t=3时,f(t)取得最大值9,即投入3百万元的广告费时,该公司由此增加的收益最大.
(Ⅱ)用于技术改造的资金为x百万元,则用于广告促销的资金为(5-x)百万元,设由此增加的收益是g(x)百万元.
则![]() .
.
![]() .
.
则当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴当x=4时,g(x)取得最大值.
即4百万元用于技术改造,1百万元用于广告促销,该公司由此增加的收益最大.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() (点
(点![]() 在
在![]() 轴上方),斜率为
轴上方),斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,且
,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)设椭圆![]() 的离心率为
的离心率为![]() ,当点
,当点![]() 为椭圆
为椭圆![]() 的右顶点时,
的右顶点时,![]() 的坐标为
的坐标为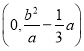 ,求
,求![]() 的值.
的值.
(2)若椭圆![]() 的方程为
的方程为![]() ,且
,且![]() ,是否存
,是否存![]() 在使得
在使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数集![]() 由实数构成,且满足:若
由实数构成,且满足:若![]() (
(![]() 且
且![]() ),则
),则![]() .
.
(1)若![]() ,试证明
,试证明![]() 中还有另外两个元素;
中还有另外两个元素;
(2)集合![]() 是否为双元素集合,并说明理由;
是否为双元素集合,并说明理由;
(3)若![]() 中元素个数不超过8个,所有元素的和为
中元素个数不超过8个,所有元素的和为![]() ,且
,且![]() 中有一个元素的平方等于所有元素的积,求集合
中有一个元素的平方等于所有元素的积,求集合![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二理科1班共有50名学生参加学业水平模拟考试,成绩(单位:分,满分100分)大于或等于90分的为优秀,其中语文成绩近似服从正态分布![]() ,数学成绩的频率分布直方图如图.
,数学成绩的频率分布直方图如图.
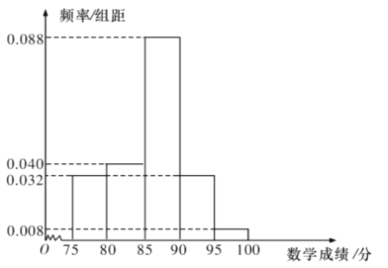
(1)这50名学生中本次考试语文、数学成绩优秀的大约各有多少人?
(2)如果语文和数学两科成绩都优秀的共有4人,从语文优秀或数学优秀的这些同学中随机抽取3人,设3人中两科都优秀的有X人,求X的分布列和数学期望;
(3)根据(1)(2)的数据,是否有99%以上的把握认为语文成绩优秀的同学,数学成绩也优秀?
语文优秀 | 语文不优秀 | 合计 | |
数学优秀 | |||
数学不优秀 | |||
合计 |
附:①若![]() ,则
,则![]() ,
,![]() ;②
;②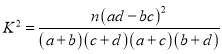 ;
;
③
| 0.1 | 0.05 | 0.025 | 0.010 | p>0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1是某条公共汽车线路收支差额![]() 与乘客量的图象.由于目前本条线路亏损,公司有关人员提出了两种扭亏为盈的建议,如图2、3所示.你能根据图象判断下列说法正确的是( )
与乘客量的图象.由于目前本条线路亏损,公司有关人员提出了两种扭亏为盈的建议,如图2、3所示.你能根据图象判断下列说法正确的是( )
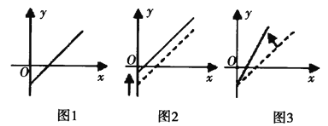
①图2的建议为减少运营成本;②图2的建议可能是提高票价;
③图3的建议为减少运营成本;④图3的建议可能是提高票价.
A.①④B.②④C.①③D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设国家收购某种农产品的价格是1.2元/kg,其中征税标准为每100元征8元(即税率为8个百分点,8%),计划可收购![]() kg.为了减轻农民负担,决定税率降低
kg.为了减轻农民负担,决定税率降低![]() 个百分点,预计收购可增加
个百分点,预计收购可增加![]() 个百分点.
个百分点.
(1)写出税收![]() (元)与
(元)与![]() 的函数关系;
的函数关系;
(2)要使此项税收在税率调节后不低于原计划的78%,确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为
的棱长为![]() ,点E,F,G分别为棱AB,
,点E,F,G分别为棱AB,![]() ,
,![]() 的中点,下列结论中,正确结论的序号是___________.
的中点,下列结论中,正确结论的序号是___________.
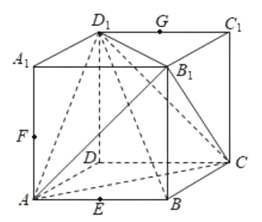
①过E,F,G三点作正方体的截面,所得截面为正六边形;
②![]() 平面EFG;
平面EFG;
③![]() 平面
平面![]() ;
;
④异面直线EF与![]() 所成角的正切值为
所成角的正切值为![]() ;
;
⑤四面体![]() 的体积等于
的体积等于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题![]() :实数
:实数![]() 满足不等式
满足不等式![]() ,命题
,命题![]() :函数
:函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知“![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() :
:![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求正整数
的必要不充分条件,求正整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com