
【题目】如图![]() ,直角梯形
,直角梯形![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折起来,使平面
折起来,使平面![]() 平面
平面![]() .如图
.如图![]() ,设
,设![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 的中点为
的中点为![]() .
.
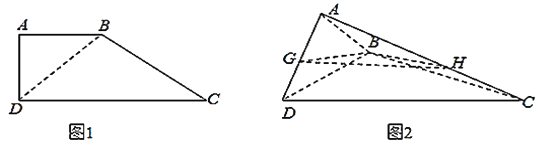
(![]() )求证:
)求证:![]() 平面
平面![]() .
.
(![]() )求平面
)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(![]() )在线段
)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在确定点
,若存在确定点![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)不存在,理由见解析.
;(3)不存在,理由见解析.
【解析】
(1)通过面面垂直的性质证得;
(2)建立空间直角坐标系,计算出两个半平面的法向量所成角的余弦值即可得解;
(3)假设存在,设出点的坐标,利用![]() 求解,找出矛盾.
求解,找出矛盾.
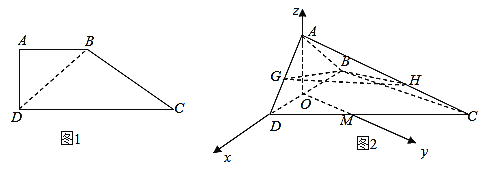
(1)![]() ,
,![]() 的中点为
的中点为![]() ,连接
,连接![]() ,必有
,必有![]() ,
,
由题:平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
,![]() 平面
平面![]() ,
,
根据面面垂直的性质可得![]() 平面
平面![]() ;
;
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
由图1直角梯形可知,![]() 为正方形,
为正方形,![]()
![]() ,
,
所以![]()
由(1)![]() 平面
平面![]() ,所以
,所以![]() 两两互相垂直,分别以
两两互相垂直,分别以![]() 为
为![]() 轴的正方向建立空间直角坐标系如图所示,
轴的正方向建立空间直角坐标系如图所示,
则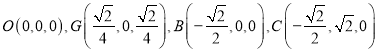 ,
,![]() ,
,
所以![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,取
,取![]() ,则
,则![]()
即平面![]() 的法向量为
的法向量为![]() ,
,![]() 平面
平面![]() ,
,
取平面![]() 的法向量
的法向量![]()
平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值 ;
;
(3)假设线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,设
,设![]() ,
,
所以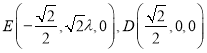 ,必有
,必有![]()
即![]() ,
,![]() ,解得
,解得![]() ,与
,与![]() 矛盾,
矛盾,
所以线段![]() 上不存在点
上不存在点![]() ,使得
,使得![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图如图所示, 支持“延迟退休年龄政策”的人数与年龄的统计结果如表:

年龄(岁) |
|
|
|
|
|
支持“延迟退休年龄政策”人数 | 15 | 5 | 15 | 28 | 17 |
(I)由以上统计数据填写下面的![]() 列联表;
列联表;
年龄低于45岁的人数 | 年龄不低于45岁的人数 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(II)通过计算判断是否有![]() 的把握认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度有差异.
的把握认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度有差异.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取![]() 名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
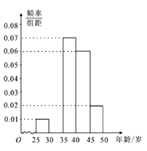
(1)求频率分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,按年龄进行分层抽样,抽取
名市民中,按年龄进行分层抽样,抽取![]() 人参加国产手机用户体验问卷调查,现从这
人参加国产手机用户体验问卷调查,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送精美礼品一份,设这
人各赠送精美礼品一份,设这![]() 名市民中年龄在
名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中有![]() 个白球和
个白球和![]() 个红球(
个红球(![]() ,且
,且![]() ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含![]() 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率![]() ;
;
(2)若![]() ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为![]() ,当
,当![]() 为何值时,
为何值时,![]() 取最大值.
取最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
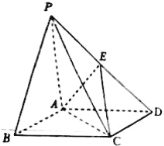
【题目】如图,在四棱锥P—ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC,PB=PD=![]() AC,E是PD的中点,求证:
AC,E是PD的中点,求证:
(1)PB∥平面ACE;
(2)平面PAC⊥平面ABCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com