
(本小题满分22分)
将m位性别相同的客人,按如下方法入住A1、A2、…、A n共n个房间。首先,安排1位客人和余下的客人![]() 的入住房间A1;然后,从余下的客人中安排2位和再次余下的客人
的入住房间A1;然后,从余下的客人中安排2位和再次余下的客人![]() 的入住房间A2;依此类推,第几号房间就安排几位客人和余下的客人
的入住房间A2;依此类推,第几号房间就安排几位客人和余下的客人![]() 的入住;这样,最后一间房间A n正好安排最后余下的n位客人。试求客人的数目和客房的数目,以及每间客房入住客人的数目。
的入住;这样,最后一间房间A n正好安排最后余下的n位客人。试求客人的数目和客房的数目,以及每间客房入住客人的数目。
解析:设安排完第k号客房A k后还剩下a k位客人,则a0=m,an-1= n…(4分)
因为第k号客房A k入住的客人数为![]() ,
,
所以![]()
![]() ,即
,即![]() ……………………(8分)
……………………(8分)
变形得![]() .
.
这表明数列b k=a k+6k-36是等比数列,公比q=![]() ,
,
其中b0=a 0-36=m-36,bn-l= a n-l+6 (n-1)-36=7n一42. ……(12分)
代入通项公式得7n一42=![]() ,
,
即 ![]() ………………(16分)
………………(16分)
由于m为正整数, 并且![]() 与
与![]() 互质,故
互质,故![]() |(n一6),
|(n一6),
但 ![]()
解得n=6,从而m=36.………………………………………………(20分)
由此可知,客房A1入住l+![]() = 6位客人;客房A2入住2+
= 6位客人;客房A2入住2+![]() =6位客人;客房A3入住3+
=6位客人;客房A3入住3+![]() =6位客人;客房A4入住4+
=6位客人;客房A4入住4+![]() =6位客人;客房A5人住5+
=6位客人;客房A5人住5+![]() =6位客人;最后一间客房人住了剩下的6位客人.
=6位客人;最后一间客房人住了剩下的6位客人.
综上可知,共有客人36人,客房6间,每间客房均入住6位客人.…(22分)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
(本小题满分22分)
设A、B分别为椭圆![]()
![]() 和双曲线
和双曲线![]() 的公共的左、右顶点。P、Q分别为双曲线和椭圆上不同于A、B的动点,且满足
的公共的左、右顶点。P、Q分别为双曲线和椭圆上不同于A、B的动点,且满足![]()
![]() 。设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4.
。设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4.
(1)求证:k1+k2+k3+k4=0;
(2)设 F1、F2分别为椭圆和双曲线的右焦点。若![]() ,求
,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年云南省高三第一次月考理科数学 题型:解答题
请考生在第22~24三题中任选一题作答,如果多做,则按所做的第一题记分.
(本小题满分10分)选修4-1:几何证明选讲
如图, 是⊙O的一条切线,切点为
是⊙O的一条切线,切点为 ,
,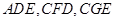 都是⊙O的割线,已知
都是⊙O的割线,已知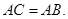 证明:
证明:

(Ⅰ) ;
;
(Ⅱ)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省郑州市高三第一次质量预测数学理卷 题型:解答题
请考生在22、23两题中任选一题作答,如果都做,则按所做的第一题记分。
(本小题满分10分)选修4-1:几何证明选讲
如图,AB是⊙O的直径,C、F为⊙O上的点,CA是∠BAF的角平分线,过点C
作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M。
(I)求证:DC是⊙O的切线; (II)求证:AM:MB=DF·DA。

查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省汕头市高三四校联考数学理卷 题型:解答题
.(本小题满分14分)
某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
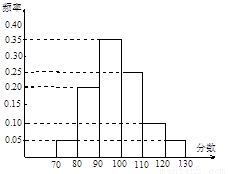
(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com