
【题目】三棱锥![]() 中,
中,![]() ,△
,△![]() 为等边三角形,二面角
为等边三角形,二面角![]() 的余弦值为
的余弦值为![]() ,当三棱锥的体积最大时,其外接球的表面积为
,当三棱锥的体积最大时,其外接球的表面积为![]() .则三棱锥体积的最大值为( )
.则三棱锥体积的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由已知作出图象,找出二面角![]() 的平面角,设出
的平面角,设出![]() 的长,即可求出三棱锥
的长,即可求出三棱锥![]() 的高,然后利用基本不等式即可确定三棱锥体积的最大值(用含有
的高,然后利用基本不等式即可确定三棱锥体积的最大值(用含有![]() 长度的字母表示),再设出球心
长度的字母表示),再设出球心![]() ,由球的表面积求得半径,根据球的几何性质,利用球心距,半径,底面半径之间的关系求得
,由球的表面积求得半径,根据球的几何性质,利用球心距,半径,底面半径之间的关系求得![]() 的长度,则三棱锥体积的最大值可求.
的长度,则三棱锥体积的最大值可求.

如图所示,过点![]() 作
作![]() 面
面![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
则![]() 为二面角
为二面角![]() 的平面角的补角,即有
的平面角的补角,即有![]() ,
,
易知![]() 面
面![]() ,则
,则![]() ,而△
,而△![]() 为等边三角形,
为等边三角形,
∴![]() 为
为![]() 中点,
中点,
设![]() ,
,
则![]() c
c![]() ,
,
故三棱锥![]() 的体积为:
的体积为:![]()
![]() ,
,
当且仅当![]() 时,体积最大,此时
时,体积最大,此时![]() 共线.
共线.
设三棱锥![]() 的外接球的球心为
的外接球的球心为![]() ,半径为
,半径为![]() ,
,
由已知,![]() ,得
,得![]() .
.
过点![]() 作
作![]() 于F,则四边形
于F,则四边形![]() 为矩形,
为矩形,
则![]() ,
, ![]() ,
,![]() ,
,
在![]() △
△![]() 中
中![]() ,解得
,解得![]()
∴三棱锥![]() 的体积的最大值为:
的体积的最大值为:![]() .
.
故选:D.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 、
、![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 、
、![]() 的中点,
的中点,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,则( )
,则( )
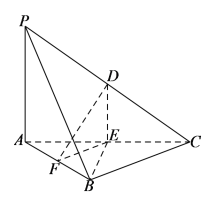
A.三棱锥![]() 的体积为
的体积为![]()
B.直线![]() 与直线
与直线![]() 垂直
垂直
C.平面![]() 截三棱锥
截三棱锥![]() 所得的截面面积为
所得的截面面积为![]()
D.点![]() 与点
与点![]() 到平面
到平面![]() 的距离相等
的距离相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.已知曲线
轴正半轴为极轴建立极坐标系.已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是
是![]() 与
与![]() 的一个交点,其极坐标为
的一个交点,其极坐标为![]() .设射线
.设射线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,与曲线
两点,与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为实现2020年全面建设小康社会,某地进行产业的升级改造.经市场调研和科学研判,准备大规模生产某高科技产品的一个核心部件,目前只有甲、乙两种设备可以独立生产该部件.如图是从甲设备生产的部件中随机抽取400件,对其核心部件的尺寸x,进行统计整理的频率分布直方图.
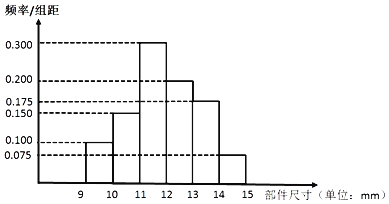
根据行业质量标准规定,该核心部件尺寸x满足:|x﹣12|≤1为一级品,1<|x﹣12|≤2为二级品,|x﹣12|>2为三级品.
(Ⅰ)现根据频率分布直方图中的分组,用分层抽样的方法先从这400件样本中抽取40件产品,再从所抽取的40件产品中,抽取2件尺寸x∈[12,15]的产品,记ξ为这2件产品中尺寸x∈[14,15]的产品个数,求ξ的分布列和数学期望;
(Ⅱ)将甲设备生产的产品成箱包装出售时,需要进行检验.已知每箱有100件产品,每件产品的检验费用为50元.检验规定:若检验出三级品需更换为一级或二级品;若不检验,让三级品进入买家,厂家需向买家每件支付200元补偿.现从一箱产品中随机抽检了10件,结果发现有1件三级品.若将甲设备的样本频率作为总体的慨率,以厂家支付费用作为决策依据,问是否对该箱中剩余产品进行一一检验?请说明理由;
(Ⅲ)为加大升级力度,厂家需增购设备.已知这种产品的利润如下:一级品的利润为500元/件;二级品的利润为400元/件;三级品的利润为200元/件.乙种设备产品中一、二、三级品的概率分别是![]() ,
,![]() ,
,![]() .若将甲设备的样本频率作为总体的概率,以厂家的利润作为决策依据.应选购哪种设备?请说明理由.
.若将甲设备的样本频率作为总体的概率,以厂家的利润作为决策依据.应选购哪种设备?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为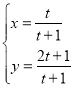 (t为参数),曲线C2的参数方程为
(t为参数),曲线C2的参数方程为![]() (α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(Ⅰ)求曲线C1的普通方程和曲线C2的极坐标方程;
(Ⅱ)射线![]() 与曲线C2交于O,P两点,射线
与曲线C2交于O,P两点,射线![]() 与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,将曲线
为参数,将曲线![]() 经过伸缩变换
经过伸缩变换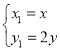 后得到曲线
后得到曲线![]() .在以原点为极点,
.在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)说明曲线![]() 是哪一种曲线,并将曲线
是哪一种曲线,并将曲线![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上的任意一点,又直线
上的任意一点,又直线![]() 上有两点
上有两点![]() 和
和![]() ,且
,且![]() ,又点
,又点![]() 的极角为
的极角为![]() ,点
,点![]() 的极角为锐角.求:
的极角为锐角.求:
①点![]() 的极角;
的极角;
②![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设α,β是空间中的两个平面,l,m是两条直线,则使得α∥β成立的一个充分条件是( )
A.lα,mβ,l∥mB.l⊥m,l∥α,m⊥β
C.lα,mα,l∥β,m∥βD.l∥m,l⊥α,m⊥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年某省将实行“![]() ”的新高考模式,即语文、数学、英语三科必选,物理、历史二选一,化学、生物、政治、地理四选二,若甲同学选科没有偏好,且不受其他因素影响,则甲同学同时选择历史和化学的概率为________
”的新高考模式,即语文、数学、英语三科必选,物理、历史二选一,化学、生物、政治、地理四选二,若甲同学选科没有偏好,且不受其他因素影响,则甲同学同时选择历史和化学的概率为________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com