
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC= ![]() .
. 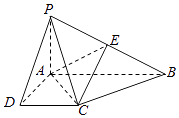
(1)求证:平面PAD⊥平面PCD;
(2)试在棱PB上确定一点E,使截面AEC把该几何体分成的两部分PDCEA与EACB的体积比为2:1;
(3)在(2)的条件下,求二面角E﹣AC﹣P的余弦值.
【答案】
(1)证明:∵AD⊥AB,DC∥AB,∴DC⊥AD,
∵PA⊥平面ABCD,DC平面ABCD,∴DC⊥PA,
∵AD∩PA=A,∴DC⊥平面PAD,
∵DC平面PCD,
∴平面PAD⊥平面PCD
(2)解:作EF⊥AB于F点,

在△ABP中,PA⊥AB,∴EF∥PA,
∴EF⊥平面ABCD,
设EF=h,AD= ![]() =1,
=1, ![]() ,
,
则 ![]() ,
,
![]() =
= ![]() =
= ![]() ,
,
由VPDCEA:VEACB=2:1,得( ![]() ):
): ![]() =2:1,解得h=
=2:1,解得h= ![]() ,
,
EF= ![]() PA,故E为PB的中点
PA,故E为PB的中点
(3)解:连结FC,FD,FD与AC交于点O,连结OE,

由(2)知EF⊥平面ABCD,∴EF⊥AC,
∵ADCF为正方形,∴FO⊥AC,
∵FO∩EF=F,
∴AC⊥平面EFO,∴EO⊥AC,
∴∠EOF是二面角E﹣AC﹣B的平面角,
∵PA⊥平面ABCD,∴平面PAC⊥平面ABCD,
∴二面角E﹣ACB与二面角E﹣AC﹣P互余,
设二面角E﹣AC﹣P的平面角为θ,
则cosθ=sin∠EOF,
在Rt△EOF中,EF= ![]() ,FO=
,FO= ![]() ,EO=
,EO= ![]() ,
,
cosθ=sin ![]() ,
,
∴二面角E﹣AC﹣P的余弦值为 ![]()
【解析】(1)推导出DC⊥AD,DC⊥PA,由此能证明平面PAD⊥平面PCD.(2)作EF⊥AB于F点,则EF⊥平面ABCD,设EF=h,由VPDCEA:VEACB=2:1,解得h= ![]() ,从而得到E为PB的中点.(3)连结FC,FD,FD与AC交于点O,连结OE,推导出EF⊥AC,FO⊥AC,EO⊥AC,从而∠EOF是二面角E﹣AC﹣B的平面角,由二面角E﹣ACB与二面角E﹣AC﹣P互余,能求出二面角E﹣AC﹣P的余弦值.
,从而得到E为PB的中点.(3)连结FC,FD,FD与AC交于点O,连结OE,推导出EF⊥AC,FO⊥AC,EO⊥AC,从而∠EOF是二面角E﹣AC﹣B的平面角,由二面角E﹣ACB与二面角E﹣AC﹣P互余,能求出二面角E﹣AC﹣P的余弦值.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2 ![]() +
+ ![]() sinωx﹣
sinωx﹣ ![]() (ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
(ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
A.(0, ![]() ]
]
B.(0, ![]() ]∪[
]∪[ ![]() ,1)
,1)
C.(0, ![]() ]
]
D.(0, ![]() ]∪[
]∪[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.

(1)求在未来的连续4天中,有2天的日销售量低于100枝且另外2天不低于150枝的概率;
(2)用![]() 表示在未来4天里日销售量不低于100枝的天数,求随机变量
表示在未来4天里日销售量不低于100枝的天数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四棱锥底面为正方形,顶点在底面的射影为正方形的中心,且该四棱锥的体积为9,当其外接球表面积最小时,它的高为( )
A.3
B.2 ![]()
C.2 ![]()
D.3 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题: 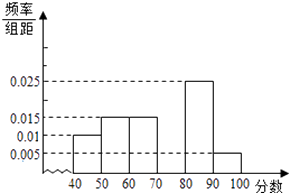
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣3)2+(y﹣4)2=4,直线l过定点A(1,0).
(1)若l与圆C相切,求l的方程;
(2)若l与圆C相交于P、Q两点,若|PQ|=2 ![]() ,求此时直线l的方程.
,求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一直线l过直线l1:3x﹣y=3和直线l2:x﹣2y=2的交点P,且与直线l3:x﹣y+1=0垂直.
(1)求直线l的方程;
(2)若直线l与圆心在x正半轴上的半径为 ![]() 的圆C相切,求圆C的标准方程.
的圆C相切,求圆C的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形ABCD中,AB=2,AD=1,M为CD的中点.如图将△ADM沿AM折起,使得平面ADM⊥平面ABCM. 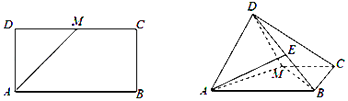
(1)求证:BM⊥平面ADM;
(2)若点E是线段DB上的中点,求三棱锥E﹣ABM的体积V1与四棱锥D﹣ABCM的体积V2之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算题
(1)已知cos( ![]() +x)=
+x)= ![]() ,(
,( ![]() <x<
<x< ![]() ),求
),求 ![]() 的值.
的值.
(2)若 ![]() ,
, ![]() 是夹角60°的两个单位向量,求
是夹角60°的两个单位向量,求 ![]() =2
=2 ![]() +
+ ![]() 与
与 ![]() =﹣3
=﹣3 ![]() +2
+2 ![]() 的夹角.
的夹角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com