
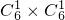 个,记事件A为“甲乙两人一次竞猜成功”,若|a-b|=0,则共有6种竞猜成功;若|a-b|=1,a=1,2,3,4时,b分别有2个值,而a=0或5时,b只有一种取值.利用古典概型的概率计算公式即可得出P(A)=
个,记事件A为“甲乙两人一次竞猜成功”,若|a-b|=0,则共有6种竞猜成功;若|a-b|=1,a=1,2,3,4时,b分别有2个值,而a=0或5时,b只有一种取值.利用古典概型的概率计算公式即可得出P(A)=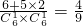 .
.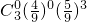 -
-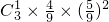 =
=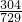 .
.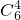 种选法,双胞胎的对数X的取值为0,1,2.
种选法,双胞胎的对数X的取值为0,1,2.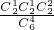 =
= ,P(X=1)=
,P(X=1)=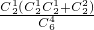 =
= ,P(X=2)=
,P(X=2)=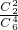 =
= .
.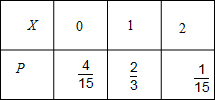
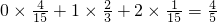 .
.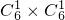 个,记事件A为“甲乙两人一次竞猜成功”,分|a-b|=0和|a-b|=1.利用古典概型的概率计算公式即可得出P(A)=
个,记事件A为“甲乙两人一次竞猜成功”,分|a-b|=0和|a-b|=1.利用古典概型的概率计算公式即可得出P(A)=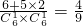 .设随机变量ξ表示在3次竞猜中竞猜成功的次数,则ξ~B
.设随机变量ξ表示在3次竞猜中竞猜成功的次数,则ξ~B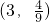 .则甲乙两人获奖的概率P(ξ≥2)=1-P(ξ=0)-P(ξ=1).
.则甲乙两人获奖的概率P(ξ≥2)=1-P(ξ=0)-P(ξ=1).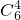 种选法,双胞胎的对数X的取值为0,1,2.X=0,表示的是分别从2对双胞胎中各自选取一个,再把不是双胞胎的2人都取来;X=1,表示的是从2对双胞胎中选取一对,另外2人的选取由两种方法,一种是把不是双胞胎的2人都选来,另一种是从另一双胞胎中选一个,从不是双胞胎的2人中选一个;X=2,表示的是把2对双胞胎2人都选来.据此即可得出X的分布列和EX.
种选法,双胞胎的对数X的取值为0,1,2.X=0,表示的是分别从2对双胞胎中各自选取一个,再把不是双胞胎的2人都取来;X=1,表示的是从2对双胞胎中选取一对,另外2人的选取由两种方法,一种是把不是双胞胎的2人都选来,另一种是从另一双胞胎中选一个,从不是双胞胎的2人中选一个;X=2,表示的是把2对双胞胎2人都选来.据此即可得出X的分布列和EX.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 11 |
| 25 |
| 11 |
| 25 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建师大附中高二(下)期末数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com