
【题目】某地区为了调查高粱的高度、粒的颜色与产量的关系,对700棵高粱进行抽样调查,得到高度频数分布表如下:
表1:红粒高粱频数分布表
农作物高度( |
|
|
|
|
|
|
频 数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:白粒高粱频数分布表
农作物高度( |
|
|
|
|
|
|
频 数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)估计这700棵高粱中红粒高粱的棵数;
(2)估计这700棵高粱中高粱高(![]() )在
)在![]() 的概率;
的概率;
(3)在样本的红粒高粱中,从高度(单位:![]() )在
)在![]() 中任选3棵,设
中任选3棵,设![]() 表示所选3棵中高(单位:
表示所选3棵中高(单位:![]() )在
)在![]() 的棵数,求
的棵数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
【答案】(1)400;(2)0.6;(3)见解析.
【解析】
(1)样本中红粒高粱为40棵,白粒高粱30棵,由抽样比例可得这亩地中红粒高粱棵数为400.
(2)样本中高在[165,180)的棵数为42,样本容量为70,由此能求出样本中高在[165,180)的频率.
(3)![]() 的可能值为
的可能值为![]() ,由超几何分布计算出可能取值的概率,列出分布列和求出期望即可.
,由超几何分布计算出可能取值的概率,列出分布列和求出期望即可.
(1)样本中红粒高粱为40棵,白粒高粱30棵,所以红粒高粱棵数大约为![]() (棵)
(棵)
(2)由表1、表2可知,样本中高在![]() 的棵数为:
的棵数为:![]() ,样本容量为70,
,样本容量为70,
∴样本中高在![]() 的频率
的频率![]() .从而估计这700棵高粱中高在
.从而估计这700棵高粱中高在![]() 的概率为
的概率为![]() .
.
(3)根据题意知:![]() 的可能值为
的可能值为![]()
所以![]() ,
,
![]() ,
,
![]() ,
,
所以![]() 的分布列为
的分布列为
| 1 | 2 | 3 |
|
|
|
|
所以![]() .
.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如表:
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
已知![]() .
.
(I)求表格中![]() 的值;
的值;
(II)从这![]() 年中随机抽取两年,求平均每台设备每年的维护费用至少有
年中随机抽取两年,求平均每台设备每年的维护费用至少有![]() 年多于
年多于![]() 万元的概率;
万元的概率;
(Ⅲ)求![]() 关于
关于![]() 的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过
的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过![]() 万元.
万元.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式:
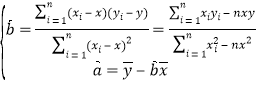
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 任作一条直线
任作一条直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() .在
.在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京某附属中学为了改善学生的住宿条件,决定在学校附近修建学生宿舍,学校总务办公室用1000万元从政府购得一块廉价土地,该土地可以建造每层1000平方米的楼房,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高![]() 万元,已知建筑第5层楼房时,每平方米建筑费用为
万元,已知建筑第5层楼房时,每平方米建筑费用为![]() 万元.
万元.
![]() 若学生宿舍建筑为x层楼时,该楼房综合费用为y万元,综合费用是建筑费用与购地费用之和
若学生宿舍建筑为x层楼时,该楼房综合费用为y万元,综合费用是建筑费用与购地费用之和![]() ,写出
,写出![]() 的表达式;
的表达式;
![]() 为了使该楼房每平方米的平均综合费用最低,学校应把楼层建成几层?此时平均综合费用为每平方米多少万元?
为了使该楼房每平方米的平均综合费用最低,学校应把楼层建成几层?此时平均综合费用为每平方米多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底而
中,底而![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 上的动点(
上的动点(![]() ,
,![]() 与所在棱的端点不重合),且满足
与所在棱的端点不重合),且满足![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值
的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A. 命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B. 若![]() 为假命题,则
为假命题,则![]() 均为假命题
均为假命题
C. 对于命题![]() :
:![]()
![]() ,使得
,使得![]() ,则
,则![]() :
:![]()
![]() ,均有
,均有![]()
D. “![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com