
【题目】成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)数列{bn}的前n项和为Sn,求证:数列{Sn+![]() }是等比数列.
}是等比数列.
【答案】(Ⅰ)![]() (Ⅱ)详见解析
(Ⅱ)详见解析
【解析】
试题分析:(I)利用成等差数列的三个正数的和等于15可设三个数分别为5-d,5,5+d,代入等比数列中可求d,进一步可求数列{bn}的通项公式;(II)根据(I)及等比数列的前 n项和公式可求![]() ,要证数列
,要证数列![]() 是等比数列
是等比数列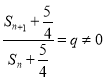 即可
即可
试题解析:(I)设成等差数列的三个正数分别为a﹣d,a,a+d
依题意,得a﹣d+a+a+d=15,解得a=5
所以{bn}中的依次为7﹣d,10,18+d
依题意,有(7﹣d)(18+d)=100,解得d=2或d=﹣13(舍去)
故{bn}的第3项为5,公比为2
由b3=b122,即5=4b1,解得![]()
所以{bn}是以![]() 首项,2为公比的等比数列,通项公式为
首项,2为公比的等比数列,通项公式为![]() ……………6分
……………6分
(II)数列{bn}的前和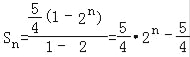
即![]() ,所以
,所以![]() ,
,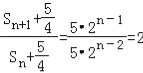
因此{![]() }是以
}是以![]() 为首项,公比为2的等比数列 …………………12分
为首项,公比为2的等比数列 …………………12分


科目:高中数学 来源: 题型:
【题目】某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
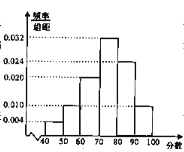
(1)若该校高二年级共有学生1000人,试估计成绩不低于60分的人数;
(2)求该校高二年级全体学生期中考试成绩的众数、中位数和平均数的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有编号分别为1,2,3,4,5的五道不同的政治题和编号分别为6,7,8,9的四道不同的历史题.甲同学从这九道题中一次性随机抽取两道题,每道题被抽到的概率是相等的,用符号(x,y)表示事件“抽到的两道题的编号分别为x,y,且x<y.”.
(1)问有多少个基本事件,并列举出来;
(2)求甲同学所抽取的两道题的编号之和小于17但不小于11的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx(a≠0)的导函数f′(x)=-2x+7,数列{an}的前n项和为Sn,点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,求数列{an}的通项公式及Sn的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com