
����Ŀ��2018���¿α������������߿������ѡ�����������ģ�����ѡ���⣺���8С�⣬ÿС��6�֣���48�֣���ÿС��������ĸ�ѡ���У���14~18��ֻ��һ�������ĿҪ��.��19��21���ж��������ĿҪ��ȫ��ѡ�Եĵ�6�֣�ѡ�Ե���ȫ�ĵ�3�֣���ѡ���ĵ�0�֣�ÿ��߿����ÿ��ĵ÷��������һ�����µ�ͳ�ƣ��صضԵ�19��ĵ÷���������У���ijʡ�����Ծ��������ȡ1000���Ծ������е�19��ĵ÷��������Ϊ1000������.ͳ�ƽ�����±���
�÷� | 0 | 3 | 6 |
���� | 200 | 300 | 500 |
��1������1000���Ծ��е�19��ĵ÷ֵ���λ����ƽ������
��2����ijУ����������ѧ�����δ�μӿ��ԣ����������ѧ���μӿ��ԣ��������и��ֵ÷������Ƶ����Ϊ������ͬѧ��Ӧ�ĸ��ֵ÷�����ĸ���.����������ͬѧ���۾���19��ĵ÷�֮��![]() �ķֲ��м�Чѧ����.
�ķֲ��м�Чѧ����.
���𰸡���1����λ����![]() ��ƽ����
��ƽ����![]() ����2���ֲ��м�������
����2���ֲ��м�������![]()
��������
��1����500λ���501λ��λ���ֵ�ƽ����������λ������500λ�÷���3�֣���501λ�÷���6��.�ɱ������ݵ�ƽ�������ü�Ȩƽ�������м���.
��2���������и��ֵ÷������Ƶ����Ϊ������ͬѧ��Ӧ�ĸ��ֵ÷�����ĸ��ʣ����0�ֵĸ���Ϊ0.2����3�ֵĸ���Ϊ0.3����6�ֵĸ���Ϊ0.5��![]() �����п���ȡֵ���Ϊ��0��3��6��9��12.������������ĸ��ʼ���ɵ÷ֲ��м�Чѧ����.
�����п���ȡֵ���Ϊ��0��3��6��9��12.������������ĸ��ʼ���ɵ÷ֲ��м�Чѧ����.
��1����Ϊ�÷���1000λ���ݣ�
������λ���Ǵ�С���������ĵ�500λ���501λ��λ���ֵ�ƽ����.
����1000���Ծ��е�19��ĵ÷ֵ���λ����![]() .
.
���У����ѧ���������Ծ��е�19���ƽ����![]() ��
��
���ɱ������ݿɵ�![]() .
.
�ݴ˿ɹ��Ƹ�ʡ����ѧ���ڱ��θ߿����۾��е�19���ƽ����Ϊ3.9��.
��2�������⣬��0�ֵĸ���Ϊ0.2����3�ֵĸ���Ϊ0.3����6�ֵĸ���Ϊ0.5��
��֪![]() �����п���ȡֵ���Ϊ��0��3.6��9��12.
�����п���ȡֵ���Ϊ��0��3.6��9��12.
��![]() ��ʾ��������ѧ������0�֣���
��ʾ��������ѧ������0�֣���![]() ��
��
![]() ��ʾ��������ѧ���е�һ����0�֣���һ����3�֣�
��ʾ��������ѧ���е�һ����0�֣���һ����3�֣�
��![]() ��
��
![]() ��ʾ��������ѧ���е�һ����0�֣���һ����6�֣�����������3�֣�
��ʾ��������ѧ���е�һ����0�֣���һ����6�֣�����������3�֣�
��![]() ��
��
![]() ��ʾ��������ѧ���е�һ����3�֣���һ����6�֣�
��ʾ��������ѧ���е�һ����3�֣���һ����6�֣�
��![]() ��
��
![]() ��ʾ��������ѧ������6�֣���
��ʾ��������ѧ������6�֣���![]() .
.
��������ͬѧ��19��ĵ÷�֮��![]() �ķֲ�������
�ķֲ�������
| 0 | 3 | 6 | 9 | 12 | |
| 0.04 | 0.12 | 0.29 | 0.3 | 0.25 |
����������ͬѧ��19��ĵ÷�֮��![]() ����ѧ����Ϊ
����ѧ����Ϊ
![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ![]() �У���֪Բ
�У���֪Բ![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������
Ϊ������![]() ��.��ԭ��
��.��ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ���������Ϊ���ᣬȡ��ͬ�ij��ȵ�λ����������ϵ��ֱ��
���������Ϊ���ᣬȡ��ͬ�ij��ȵ�λ����������ϵ��ֱ��![]() �ļ����귽����
�ļ����귽����![]() .
.
��1����ֱ��![]() ��Բ
��Բ![]() �й����㣬����ʵ��
�й����㣬����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ʱ������
ʱ������![]() ����ֱ��
����ֱ��![]() ƽ�е�ֱ��
ƽ�е�ֱ��![]() ��Բ
��Բ![]() ��
��![]() ���㣬��
���㣬��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��PM2��5�Ǻ���������������Ҫָ�꣬�ҹ�����������֯�����ֵ��ֵ����PM2��5�վ�ֵ��![]() ���¿�������Ϊһ������
���¿�������Ϊһ������![]() ��������Ϊ����������
��������Ϊ����������![]() Ϊ���꣬��ͼ��ij��1��1����10�յ�PM2��5����λ��
Ϊ���꣬��ͼ��ij��1��1����10�յ�PM2��5����λ��![]() �����վ�ֵ��������˵����ȷ���ǣ� ��
�����վ�ֵ��������˵����ȷ���ǣ� ��
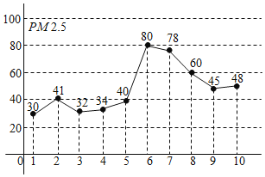
A.10����PM2��5�վ�ֵ��͵���1��3��
B.��1�յ�6��PM2��5�վ�ֵ������
C.��10����ǡ��5���������������
D.��10����PM2��5�վ�ֵ����λ����43
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������P��ABCD�У�ƽ��PAC��ƽ��ABCD������AB��DC��AC��CD��DA![]() AB.
AB.

��1��֤����BC��PA��
��2����PA��PC��AC����ƽ��PAD��ƽ��PBC���ɵ������ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������3����ȫ��50�˲μ��˸߿�ǰ����ѧģ����ԣ�ÿ��ѧ��Ҫ�ڹ涨��2��Сʱ����һ����ģ������ֳ�ȡ10λѧ���ijɼ�����Ϊ�ף������飬��������±���
1�� | 2�� | 3�� | 4�� | 5�� | |
���� | 64 | 72 | 86 | 98 | 120 |
���� | 60 | 76 | 90 | 92 | 122 |
���ֱ�����ף�������ѧ���������÷�����ƽ������������ɴ˷�������ѧ���ijɼ�ˮƽ��
�����Թ���ȫ���ж����˼���90�ּ�����Ϊ����
���Ӹð༶�ף��������и������ȡ1��ѧ�������俼�Գɼ����г�飬�����˿��Է���֮�ʹ��ڵ���180�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(��)(2017�������ģ)Ϊ��սij���˶��ᣬij���������齨��һ����4�����˶�Ա��2��Ů�˶�Ա��ɵ�6�˴����Ӳ����б�սѵ��.
(1)������սѵ������6�������ѡ��2�˽��гɹ����飬��ѡ����2����������1��Ů�˶�Ա�ĸ��ʣ�
(2)��������ס��������˶�Ա�ijɼ��þ�Ҷͼ��ʾ��ͼ��

����˵����λ�˶�Ա�ijɼ����ȶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ⳤΪ1��������![]() �����Խ���
�����Խ���![]() ��ƽ��
��ƽ��![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() �ڵ�
�ڵ�![]() �����½�����ȷ���ǣ� ��
�����½�����ȷ���ǣ� ��
A.�ı���![]() ��һ����ƽ���ı���
��һ����ƽ���ı���
B.ƽ��![]() �����������������ֵ�������
�����������������ֵ�������
C.ƽ��![]() ��ƽ��
��ƽ��![]() �����ܴ�ֱ
�����ܴ�ֱ
D.�ı���![]() ��������ֵΪ
��������ֵΪ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������
��������![]() ��
��![]() ����Բ
����Բ![]() ��һ�㣮
��һ�㣮
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ����ֱ��
����ֱ��![]() ����Բ
����Բ![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() ����ԭ��ĶԳƵ�Ϊ
����ԭ��ĶԳƵ�Ϊ![]() ����
����![]() ����Բ
����Բ![]() ��һ�㣬�ж�ֱ��
��һ�㣬�ж�ֱ��![]() ��
��![]() ��б��֮���Ƿ�Ϊ��ֵ������ǣ�������˶�ֵ��������ǣ���˵�����ɣ�
��б��֮���Ƿ�Ϊ��ֵ������ǣ�������˶�ֵ��������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD���������ij��ֱ���ȣ�����Ϊ3��4��x����x��ȡֵ��Χ��![]() ����
����![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com