
【题目】
甲、乙、丙三名射击运动员射中目标的概率分别为![]()
![]() ,三人各射击一次,击中目标的次数记为
,三人各射击一次,击中目标的次数记为![]() .
.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)在概率![]() (
(![]() =0,1,2,3)中, 若
=0,1,2,3)中, 若![]() 的值最大, 求实数
的值最大, 求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,ξ的分布列为
,ξ的分布列为
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
(2)![]()
【解析】
(1)P(ξ)是“ξ个人命中,3-ξ个人未命中”的概率.其中ξ的可能取值为0、1、2、3.
P(ξ=0)=![]()
![]()
![]() (1-a)2=
(1-a)2=![]() (1-a)2;
(1-a)2;
P(ξ=1)=![]() ·
·![]()
![]() (1-a)2+
(1-a)2+![]()
![]()
![]() a(1-a)=
a(1-a)=![]() (1-a2);
(1-a2);
P(ξ=2)=![]() ·
·![]()
![]() a(1-a)+
a(1-a)+![]()
![]()
![]() a2=
a2=![]() (2a-a2);
(2a-a2);
P(ξ=3)=![]() ·
·![]()
![]() a2=
a2=![]() .
.
所以ξ的分布列为
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
ξ的数学期望为
E(ξ)=0×![]() (1-a)2+1×
(1-a)2+1×![]() (1-a2)+2×
(1-a2)+2×![]() (2a-a2)+3×
(2a-a2)+3×![]() =
=![]() .
.
(2)P(ξ=1)-P(ξ=![]() [(1-a2)-(1-a)2]=a(1-a);
[(1-a2)-(1-a)2]=a(1-a);
P(ξ=1)-P(ξ=2)=![]() [(1-a2)-(2a-a2)]=
[(1-a2)-(2a-a2)]=![]() ;
;
P(ξ=1)-P(ξ=3)=![]() [(1-a2)-a2]=
[(1-a2)-a2]=![]() .
.
由 和0<a<1,得0<a≤
和0<a<1,得0<a≤![]() ,即a的取值范围是
,即a的取值范围是![]() .
.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() (
(![]() )的焦点为
)的焦点为![]() ,准线为
,准线为![]() ,若点
,若点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() 是周长为12的等边三角形.
是周长为12的等边三角形.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,若
,若![]() ,求直线
,求直线![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景区拟将一半径为![]() 的半圆形绿地改建为等腰梯形
的半圆形绿地改建为等腰梯形![]() (如图,其中
(如图,其中![]() 为圆心,点
为圆心,点![]() 在半圆上)的放养观赏鱼的鱼池,周围四边建成观鱼长廊(宽度忽略不计).设
在半圆上)的放养观赏鱼的鱼池,周围四边建成观鱼长廊(宽度忽略不计).设![]() ,鱼池面积为
,鱼池面积为![]() (单位:
(单位:![]() ).
).
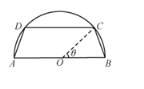
(1)求S关于![]() 的函数表达式,并求鱼池面积何时最大;
的函数表达式,并求鱼池面积何时最大;
(2)已知鱼池造价为每平方米2000元,长廊造价为每米3000元,问此次改建的最高造价不超过多少?(取![]() 计算)
计算)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正,Sn为数列{an}的前n项和,an2+2an=4Sn+3.
(1)求{an}的通项公式;
(2)设bn![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=2,点P在棱DF上.
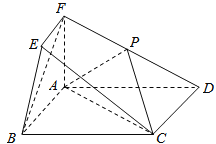
(1)若P是DF的中点,求异面直线BE与CP所成角的余弦值;
(2)若二面角D﹣AP﹣C的正弦值为![]() ,求PF的长度.
,求PF的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高).现从参赛者中抽取了![]() 人,按年龄分成5组,第一组:
人,按年龄分成5组,第一组: ![]() ,第二组:
,第二组: ![]() ,第三组:
,第三组: ![]() ,第四组:
,第四组: ![]() ,第五组:
,第五组: ![]() ,得到如图所示的频率分布直方图,已知第一组有6人.
,得到如图所示的频率分布直方图,已知第一组有6人.
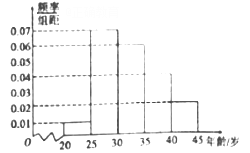
(1)求![]() ;
;
(2)求抽取的![]() 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);
(3)从该市大学生、军人、医务人员、工人、个体户 五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1~5组,从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛,分别代表相应组的成绩,年龄组中1~5组的成绩分别为93,96,97,94,90,职业组中1~5组的成绩分别为93,98,94,95,90.
(Ⅰ)分别求5个年龄组和5个职业组成绩的平均数和方差;
(Ⅱ)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com