【题目】在古代，直角三角形中较短的直角边称为“勾”,较长的直角边称为“股”，斜边称为“弦”.三国时期吴国数学家赵爽用“弦图”( 如图) 证明了勾股定理，证明方法叙述为:“按弦图,又可以勾股相乘为朱实二，倍之为朱实四，以勾股之差自相乘为中黄实，加差实，亦成弦实.”这里的“实”可以理解为面积.这个证明过程体现的是这样一个等量关系:“两条直角边的乘积是两个全等直角三角形的面积的和(朱实二 )，4个全等的直角三角形的面积的和(朱实四) 加上中间小正方形的面积(黄实) 等于大正方形的面积(弦实)”. 若弦图中“弦实”为16，“朱实一”为
,现随机向弦图内投入一粒黄豆(大小忽略不计)，则其落入小正方形内的概率为( )
A. 
B. 
C. 
D. 
100分闯关期末冲刺系列答案科目：高中数学 来源： 题型：
【题目】如图,在矩形ABCD中,AB=2BC,P是线段AB中点,
平面ABCD.
(1)求证:
平面EPC;
(2)问在EP上是否存在点F,使平面
平面BFC?若存在,求出
的值;若不存在请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某种产品的广告费用支出x(万元)与销售额y(万元)之间有如下的对应数据：
(1)画出散点图；
(2)求回归直线方程；
(3)据此估计广告费用为9万元时，销售收入y的值.
注：①参考公式：线性回归方程系数公式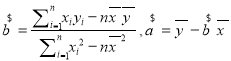
；
②参考数据：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
，
，…，
是1，2，…，
的一个排列，把排在
的左边且比小的数的个数称为
的顺序数，如在排列6，4，5，3，2，1中，5的顺序数为1，3的顺序数为0，则在1至8这8个数的排列中，8的顺序数为2，7的顺序数为3，5的顺序数为3的不同排列的种数为
A. 96B. 144C. 192D. 240
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】有
、
、
、
四位贵宾，应分别对应坐在
、
、
、
四个席位上，现在这四人均未留意，在四个席位上随便就座.
（1）求这四人恰好都坐在自己席位上的概率；
（2）求这四人恰好都没坐在自己席位上的概率；
（3）求这四人恰好有
位坐在自己席位上的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】小李在做一份调查问卷，共有4道题，其中有两种题型，一种是选择题，共2道，另一种是填空题，共2道．
（1）小李从中任选2道题解答，每一次选1题(不放回)，求所选的题不是同一种题型的概率；
（2）小李从中任选2道题解答，每一次选1题(有放回)，求所选的题不是同一种题型的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下面是追踪调查200个某种电子元件寿命（单位:
)频率分布直方图，如图：
其中300-400、400-500两组数据丢失，下面四个说法中有且只有一个与原数据相符，这个说法是( )
①寿命在300-400的频数是90；
②寿命在400-500的矩形的面积是0.2；
③用频率分布直方图估计电子元件的平均寿命为：
④寿命超过
的频率为0.3
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目：高中数学 来源： 题型：
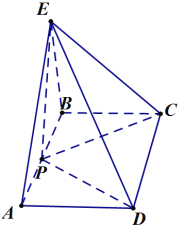
【题目】如图,在棱长均相等的四棱锥
中, 
为底面正方形的中心, 
,
分别为侧棱
,
的中点,有下列结论正确的有：( )
A.
∥平面
B.平面
∥平面
C.直线与直线
所成角的大小为
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
