
【题目】椭圆![]() 的左焦点为
的左焦点为![]() ,直线
,直线![]() 与椭圆相交于点
与椭圆相交于点![]() ,当
,当![]() 的周长最大时,
的周长最大时, ![]() 的面积是( )
的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是函数
是函数![]() 图象上的点,
图象上的点,![]() 是双曲线在第四象限这一分支上的动点,过点
是双曲线在第四象限这一分支上的动点,过点![]() 作直线,使其与双曲线
作直线,使其与双曲线![]() 只有一个公共点,且与
只有一个公共点,且与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,另一条直线
,另一条直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .
.
则(1)![]() 为坐标原点,三角形
为坐标原点,三角形![]() 的面积为__________.
的面积为__________.
(2)四边形![]() 面积的最小值为__________.
面积的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,且
,且 ![]() .
.
(1)求m的值;
(2)判断f(x)在(0,+∞)上的单调性,并给予证明;
(3)求函数f(x)在区间[﹣5,﹣1]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,且
,且![]() ,公比大于1的等比数列
,公比大于1的等比数列![]() 满足
满足![]() ,
, ![]() .
.
(1)求证数列![]() 是等差数列,并求其通项公式;
是等差数列,并求其通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在(2)的条件下,若![]() 对一切正整数
对一切正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值
的取值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ),
),![]() ,
,
(Ⅰ) 试求曲线![]() 在点
在点![]() 处的切线l与曲线
处的切线l与曲线![]() 的公共点个数;(Ⅱ) 若函数
的公共点个数;(Ⅱ) 若函数![]() 有两个极值点,求实数a的取值范围.
有两个极值点,求实数a的取值范围.
(附:当![]() ,x趋近于0时,
,x趋近于0时, ![]() 趋向于
趋向于![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( ) 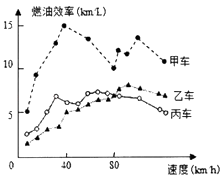
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油
D.甲车以80千米/小时的速度行驶1小时,消耗10升汽油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax﹣(m﹣2)a﹣x (a>0且a≠1)是定义域为R的奇函数.
(1)求m的值;
(2)若f(1)<0,试判断y=f(x)的单调性,并求使不等式f(x2+tx)+f(4﹣x)<0恒成立的t的取值范围;
(3)若f(1)= ![]() ,g(x)=a2x+a﹣2x﹣2f(x),求g(x)在[1,+∞)上的最小值.
,g(x)=a2x+a﹣2x﹣2f(x),求g(x)在[1,+∞)上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】潍坊文化艺术中心的观光塔是潍坊市的标志性建筑,某班同学准备测量观光塔![]() 的高度
的高度![]() (单位:米),如图所示,垂直放置的标杆
(单位:米),如图所示,垂直放置的标杆![]() 的高度
的高度![]() 米,已知
米,已知![]() ,
, ![]() .
.
(1)该班同学测得![]() 一组数据:
一组数据: ![]() ,请据此算出
,请据此算出![]() 的值;
的值;
(2)该班同学分析若干测得的数据后,发现适当调整标杆到观光塔的距离![]() (单位:米),使
(单位:米),使![]() 与
与![]() 的差较大,可以提高测量精确度,若观光塔高度为136米,问
的差较大,可以提高测量精确度,若观光塔高度为136米,问![]() 为多大时,
为多大时, ![]() 的值最大?
的值最大?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com