Question

【题目】设离心率为 的椭圆E： + =1（a＞b＞0）的左、右焦点为F1 ， F2 ， 点P是E上一点，PF1⊥PF2 ， △PF1F2内切圆的半径为 ﹣1．
（1）求E的方程；
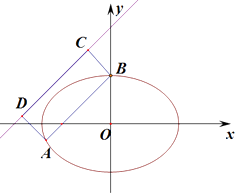
（2）矩形ABCD的两顶点C、D在直线y=x+2，A、B在椭圆E上，若矩形ABCD的周长为 ，求直线AB的方程．

Answer 1

【答案】
（1）

解：∵离心率为e= = ，则a= c，①

由PF1⊥PF2，则丨PF1丨2+丨PF2丨2=丨F1F2丨2=4c2，

由椭圆的定义可知；丨PF1丨+丨PF2丨=2a，则丨F1F2丨2=（丨PF1丨+丨PF2丨）2﹣2丨PF1丨丨PF2丨，

∴丨PF1丨丨PF2丨=2a2﹣2c2，

，△PF1F2的面积S，S= 丨PF1丨丨PF2丨= ×R×（丨PF1丨+丨PF2丨+丨F1F2丨），

则a﹣c= ﹣1．②

由①②解得：a= ，c=1，

b2=a2﹣c2=1，

∴椭圆E的方程为 ．

（2）

解：由题意设直线l的方程：y=x+m，A（x1，y1）、B（x2，y2），

则 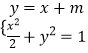，整理得：3x2+4mx+2m2﹣2=0，

由△=16m2﹣4×3（2m2﹣2）=﹣2m2+3＞0，解得﹣ ＜m＜ ，

由韦达定理可知：x1+x2=﹣ ，x1x2= ，

则丨AB丨= = = ，

直线AB，CD之间的距离d= = ，

由矩形ABCD的周长为 ，则2（丨AB丨+d）= ，

则2（ + ）= ，解得：m=1，

则直线AB的方程为y=x+1．

【解析】（1）由椭圆的离心率求得a= c，根据勾股定理及椭圆的定义，求得a﹣c= ﹣1．b2=a2﹣c2=1，即可求得椭圆的标准方程；（2）设直线l的方程，代入椭圆方程，由韦达定理及弦长公式求得丨AB丨，由两平行之间的距离公式，由矩形的周长公式2（丨AB丨+d）= ，代入即可求得m的值，求得直线AB的方程．