
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过右焦点
,过右焦点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的周长为
的周长为![]() ,点
,点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 、
、![]() 的斜率
的斜率![]() ,
,![]() ,请问
,请问![]() 是否为定值?若是定值,求出其定值;若不是,说明理由.
是否为定值?若是定值,求出其定值;若不是,说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】独立性检验中,假设![]() :运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得
:运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得![]() 的观测值
的观测值![]() .下列结论正确的是( )
.下列结论正确的是( )
附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动有关
B. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动无关
C. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动有关
D. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是_________
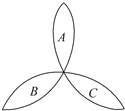
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,且函数
,且函数![]() 是偶函数.
是偶函数.
(1)求![]() 的解析式;.
的解析式;.
(2)若不等式![]() 在
在![]() 上恒成立,求n的取值范围;
上恒成立,求n的取值范围;
(3)若函数 恰好有三个零点,求k的值及该函数的零点.
恰好有三个零点,求k的值及该函数的零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足:存在正整数T,对于任意正整数n都有
满足:存在正整数T,对于任意正整数n都有![]() 成立,则称数列
成立,则称数列![]() 为周期数列,周期为T.已知数列
为周期数列,周期为T.已知数列![]() 满足
满足![]() ,
, ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A.若![]() ,则m可以取3个不同的值;
,则m可以取3个不同的值;
B.若![]() ,则数列
,则数列![]() 是周期为3的数列;
是周期为3的数列;
C.对于任意的![]() 且T≥2,存在
且T≥2,存在![]() ,使得
,使得![]() 是周期为
是周期为![]() 的数列
的数列
D.存在![]() 且
且![]() ,使得数列
,使得数列![]() 是周期数列
是周期数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年入冬以来,各地雾霾天气频发,![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于
是指直径小于或等于![]() 微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
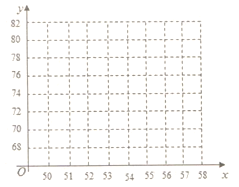
(1)请根据上述数据,在上面给出的坐标系中画出散点图;
(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,大量的统计数据表明,参与调查者中关注此问题的约占80%.现从参与调查的人群中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第1组
人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
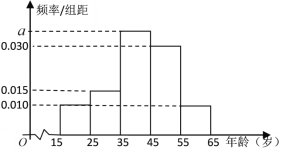
(1)求![]() 的值;
的值;
(2)求出样本的平均数(同一组数据用该区间的中点值作代表);
(3)现在要从年龄较小的第1,2组中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行问卷调查,求第2组中抽到
人进行问卷调查,求第2组中抽到![]() 人的概率.
人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com