
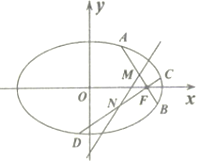
 已知椭圆$Ω:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过点$Q({\frac{{\sqrt{2}}}{2},1})$作圆x2+y2=1的切线,切点分别为S,T.直线ST恰好经过Ω的右顶点和上顶点.
已知椭圆$Ω:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过点$Q({\frac{{\sqrt{2}}}{2},1})$作圆x2+y2=1的切线,切点分别为S,T.直线ST恰好经过Ω的右顶点和上顶点.分析 (1)根据直线和圆的位置关系,可求出直线ST的方程,则直线ST恰好经过Ω的右顶点和上顶点,求出a,b的值,问题得以解决
利用椭圆的离心率,以及,|AB|+|CD|=3.求出a、b,即可求椭圆的方程;
(2)①若直线 AB,CD斜率均存在,设直线AB:y=k(x-1),A(x1,y1),B(x2,y2),根据中点坐标,以及韦达定理,即可求出k的值,即可求出点的坐标.
②当当直线AB,CD的斜率均存在且不为0时,由①可知,将直线AB的方程代入椭圆方程中,利用韦达定理以及弦长公式,求出AB,CD即可求解面积的表达式,通过基本不等式求出面积的最值.
解答 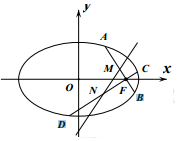 解:(1)过$({\frac{{\sqrt{2}}}{2},1})$作圆x2+y2=1的切线,一条切线为直线y=1,切点S(0,1).
解:(1)过$({\frac{{\sqrt{2}}}{2},1})$作圆x2+y2=1的切线,一条切线为直线y=1,切点S(0,1).
设另一条切线为$y-1=k({x-\frac{{\sqrt{2}}}{2}})$,即$2kx-2y+2-\sqrt{2}k=0$.
因为直线与圆x2+y2=1相切,则$\frac{{|{2-\sqrt{2}k}|}}{{\sqrt{4{k^2}+4}}}=1$.解得$k=-2\sqrt{2}$.
所以切线方程为$y=-2\sqrt{2}x+3$.
由$\left\{\begin{array}{l}y=-2\sqrt{2}x+3\\{x^2}+{y^2}=1\end{array}\right.$,解得$T({\frac{{2\sqrt{2}}}{3},\frac{1}{3}})$,
直线ST的方程为$y-1=\frac{{\frac{1}{3}-1}}{{\frac{{2\sqrt{2}}}{3}-0}}({x-0})$,
即$y=1-\frac{{\sqrt{2}}}{2}x$.
令x=0,则y=1所以上顶点的坐标为(0,1),
所以b=1;
令y=0,则$x=\sqrt{2}$,
所以右顶点的坐标为$({\sqrt{2},0})$,
所以$a=\sqrt{2}$,
所以椭圆Ω的方程为$\frac{x^2}{2}+{y^2}=1$.
(2)①若直线 AB,CD斜率均存在,设直线AB:y=k(x-1),A(x1,y1),B(x2,y2),则中点 $M({\frac{{{x_1}+{x_2}}}{2},k({\frac{{{x_1}+{x_2}}}{2}-1})})$.
先考虑k≠0的情形.由$\left\{\begin{array}{l}y=k({x-1})\\{x^2}+2{y^2}-2=0\end{array}\right.$得(1+2k2)x2-4k2x+2k2-2=0.
由直线AB过点F(1,0),可知判别式△>0恒成立.
由韦达定理,得${x_1}+{x_2}=\frac{{4{k^2}}}{{1+2{k^2}}}$,
故$M({\frac{{2{k^2}}}{{1+2{k^2}}},\frac{-k}{{1+2{k^2}}}})$,
将上式中的k换成$-\frac{1}{k}$,则同理可得$N({\frac{2}{{2+{k^2}}},\frac{k}{{2+{k^2}}}})$.
若$\frac{{2{k^2}}}{{1+2{k^2}}}=\frac{2}{{2+{k^2}}}$,得k=±1,
则直线 MN斜率不存在.此时直线MN过点$({\frac{2}{3},0})$.
②当直线AB,CD的斜率均存在且不为0时,由①可知,将直线AB的方程代入椭圆方程中,并整理得 (1+2k2)x2-4k2x+2k2-2=0,
所以$|{AB}|=\sqrt{{k^2}+1}|{{x_1}-{x_2}}|=\sqrt{{k^2}+1}\sqrt{({{x_1}+{x_2}})-4{x_1}{x_2}}=\sqrt{{k^2}+1}\sqrt{{{({\frac{{4{k^2}}}{{1+2{k^2}}}})}^2}-4×\frac{{2{k^2}-2}}{{1+2{k^2}}}}$=$\sqrt{{k^2}+1}•\frac{{2\sqrt{2}\sqrt{{k^2}+1}}}{{1+2{k^2}}}=\frac{{2\sqrt{2}({{k^2}+1})}}{{1+2{k^2}}}$.
同理,$|{CD}|=\frac{{2\sqrt{2}({\frac{1}{k^2}+1})}}{{1+\frac{2}{k^2}}}=\frac{{2\sqrt{2}({{k^2}+1})}}{{{k^2}+2}}$,
则${S_{四边形}}=\frac{1}{2}•|{AB}|•|{CD}|=\frac{1}{2}•\frac{{2\sqrt{2}\sqrt{{k^2}+1}}}{{1+2{k^2}}}•\frac{{2\sqrt{2}({{k^2}+1})}}{{{k^2}+2}}=\frac{{4{{({{k^2}+1})}^2}}}{{2{k^4}+2+5{k^2}}}$,
=$\frac{{4{{({k+\frac{1}{k}})}^2}}}{{2{k^2}+\frac{2}{k^2}+5}}=\frac{{4{{({k+\frac{1}{k}})}^2}}}{{2{{({k+\frac{1}{k}})}^2}+1}}=2-\frac{2}{{2{{({k+\frac{1}{k}})}^2}+1}}$,
因为$2{({k+\frac{1}{k}})^2}+1≥2{({2\sqrt{k•\frac{1}{k}}})^2}+1=9$,当且仅当k=±1时取等号,
所以$0<\frac{2}{{2{{({k+\frac{1}{k}})}^2}+1}}≤\frac{2}{9},\frac{16}{9}≤2-\frac{2}{{2{{({k+\frac{1}{k}})}^2}+1}}<2$,
即$\frac{16}{9}≤{S_{四边形}}<2$.
所以,由A,C,B,D四点构成的四边形面积的取值范围为$[{\frac{16}{9},2})$.
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系的应用,弦长公式的求法以及基本不等式的应用,是综合性比较强的题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
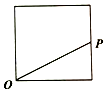 点P从点O出发,按逆时针方向沿周长为l的正方形运动一周,记O,P两点连线的距离y与点P走过的路程x为函数f(x),则y=f(x)的图象大致是( )
点P从点O出发,按逆时针方向沿周长为l的正方形运动一周,记O,P两点连线的距离y与点P走过的路程x为函数f(x),则y=f(x)的图象大致是( )| A. | 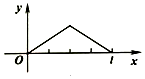 | B. | 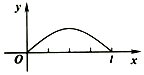 | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
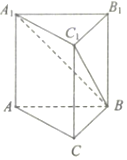 《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )| A. | $\frac{8}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $2\sqrt{6}$ | C. | $4\sqrt{3}$ | D. | $2\sqrt{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com