
分析 以小河所在直线为x轴,过点A的垂线为y轴,建立直角坐标系,点A(0,400)关于x轴的对称点A′(0,-400),由两点式得直线A′B的方程为y=$\frac{5}{4}$x-400,即可得出结论.
解答 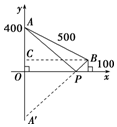 解:如图,以小河所在直线为x轴,过点A的垂线为y轴,建立直角坐标系,
解:如图,以小河所在直线为x轴,过点A的垂线为y轴,建立直角坐标系,
则点A(0,400),点B(a,100).
过点B作BC⊥AO于点C.
在△ABC中,AB=500,AC=400-100=300,
由勾股定理得BC=400,所以B(400,100).
点A(0,400)关于x轴的对称点A′(0,-400),
由两点式得直线A′B的方程为y=$\frac{5}{4}$x-400.
令y=0,得x=320,即点P(320,0).
故供水站(点P)在距O点320 m处时,到A,B两厂铺设的水管长度之和最短.
点评 本题考查利用数学知识解决实际问题,考查直线方程,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,1) | C. | (-∞,$\frac{3}{2}$] | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
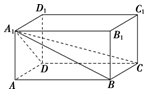
| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
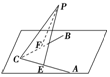 ∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2$\sqrt{3}$ cm,那么PC与平面ABC所成角的大小为45°.
∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2$\sqrt{3}$ cm,那么PC与平面ABC所成角的大小为45°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,-1} | B. | {0,1} | C. | {-1,1} | D. | {-1,0,1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com