
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .现以极点
.现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为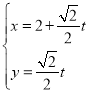 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标系方程和直线
的直角坐标系方程和直线![]() 的普通方程;
的普通方程;
(2)点![]() 在曲线
在曲线![]() 上,且到直线
上,且到直线![]() 的距离为
的距离为![]() ,求符合条件的
,求符合条件的![]() 点的直角坐标.
点的直角坐标.
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的,下列说法中正确的是( )
A.100个吸烟者中至少有99人患有肺癌
B.1个人吸烟,那么这个人有99%的概率患有肺癌
C.在100个吸烟者中一定有患肺癌的人
D.在100个吸烟者中可能一个患肺癌的人也没有
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人在相同的条件下投篮5轮,每轮甲、乙各投篮10次,投篮命中次数的情况如图所示(实线为甲的折线图,虚线为乙的折线图),则以下说法错误的是( )

A. 甲投篮命中次数的众数比乙的小
B. 甲投篮命中次数的平均数比乙的小
C. 甲投篮命中次数的中位数比乙的大
D. 甲投篮命中的成绩比乙的稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定函数![]() 和
和![]() ,若存在常数
,若存在常数![]() ,
,![]() ,使得函数
,使得函数![]() 和
和![]() 对其公共定义域
对其公共定义域![]() 的任何实数
的任何实数![]() 分别满足
分别满足![]() 和
和![]() ,则称直线
,则称直线![]() :
:![]() 为函数
为函数![]() 和
和![]() 的“隔离直线”,给出下列四组函数:
的“隔离直线”,给出下列四组函数:
(1)![]() ,
,![]() ; (2)
; (2)![]() ,
,![]() ;
;
(3)![]() ,
,![]() ; (4)
; (4)![]() ,
,![]() ;
;
其中函数![]() 和
和![]() 存在“隔离直线”的序号是( )
存在“隔离直线”的序号是( )
A.(1)(3)B.(1)(3)(4)C.(1)(2)(3)D.(2)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com