
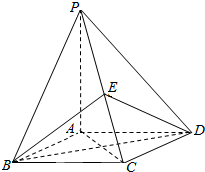
 如图4,四边形ABCD为菱形,∠ABC=60°.PA⊥平面ABCD,E为PC中点.
如图4,四边形ABCD为菱形,∠ABC=60°.PA⊥平面ABCD,E为PC中点.分析 (Ⅰ)证明面面垂直一般利用面面垂直的判定定理故可连接EO可利用中位线定理证得EO∥PC再结合PC⊥平面ABCD可得EO⊥平面ABCD即可得证.
(Ⅱ)过B作BM⊥平面ABCD,连结PM,ME,说明∠ABO计算平面PBA与平面EBD所成二面角的平面角,利用已知条件求出角的大小,即可求解余弦值.
解答 (Ⅰ)证明:连结AC交BD于点O,连结OE,则O是AC的中点.
又知E是AP中点
∴EO∥PC,
∵PC⊥平面ABCD,∴OE⊥平面ABCD.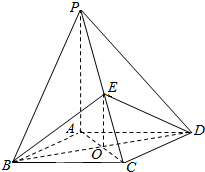
又知OE?平面BDE,
∴平面EBD⊥平面ABCD.
(Ⅱ)解:过B作BM⊥平面ABCD,连结PM,ME,如图,
由(Ⅰ)可知,PA∥EO∥MB,
则MB是平面PBA与平面EBD的交线,可得MB⊥AB,MB⊥BO,
∠ABO计算平面PBA与平面EBD所成二面角的平面角,
四边形ABCD为菱形,∠ABC=60°.可知:∠ABO=30°
cos∠ABO=cos30°=$\frac{\sqrt{3}}{2}$.
平面PBA与平面EBD所成二面角(锐角)的余弦值:$\frac{\sqrt{3}}{2}$.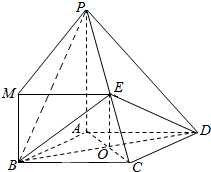
点评 本题考查PA⊥平面ABCD的证明,考查二面角A-PB-C的余弦值的求法,解题时要注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2+1 | B. | f(x)=(x+1)2+1 | C. | f(x)=(x-1)2+1 | D. | f(x)=x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
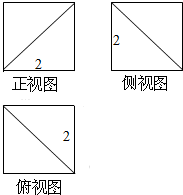
| A. | 18 | B. | 20 | C. | $18+2\sqrt{3}$ | D. | $18+4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | (1,2] | C. | [2,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com