
【题目】已知![]() 为坐标原点,双曲线
为坐标原点,双曲线![]()
![]() 上有
上有![]() 两点满足
两点满足![]() ,且点
,且点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
讨论直线![]() 的斜率是否存在:当斜率不存在时,易得直线
的斜率是否存在:当斜率不存在时,易得直线![]() 的方程,根据
的方程,根据![]() 及点O到直线
及点O到直线![]() 距离即可求得
距离即可求得![]() 的关系,进而求得离心率;当斜率存在时,设出直线方程,联立双曲线方程,结合
的关系,进而求得离心率;当斜率存在时,设出直线方程,联立双曲线方程,结合![]() 及点到直线距离即可求得离心率。
及点到直线距离即可求得离心率。
(1)当直线![]() 的斜率不存在时,由点
的斜率不存在时,由点![]() 到直线
到直线![]() 的距离为
的距离为![]() 可知直线
可知直线![]() 的方程为
的方程为![]()
所以线段![]()
因为![]() ,根据等腰直角三角形及双曲线对称性可知
,根据等腰直角三角形及双曲线对称性可知![]() ,即
,即![]()
双曲线中满足![]()
所以![]() ,化简可得
,化简可得![]() 同时除以
同时除以![]() 得
得
![]() ,解得
,解得![]()
因为![]() ,所以
,所以![]()
(2)当直线![]() 的斜率存在时,可设直线方程为
的斜率存在时,可设直线方程为
![]() ,联立方程可得
,联立方程可得
化简可得![]()
设![]()
则![]() ,
,![]()
![]()
![]()
因为点![]() 到直线
到直线![]() 的距离为
的距离为![]()
则![]() ,化简可得
,化简可得![]()
又因为![]()
所以![]()
化简得![]()
即![]()
所以![]() ,双曲线中满足
,双曲线中满足![]()
代入化简可得![]()
求得![]() ,即
,即![]()
因为![]() ,所以
,所以![]()
综上所述,双曲线的离心率为![]()
所以选A


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】现有某高新技术企业年研发费用投入![]() (百万元)与企业年利润
(百万元)与企业年利润![]() (百万元)之间具有线性相关关系,近5年的年科研费用和年利润具体数据如下表:
(百万元)之间具有线性相关关系,近5年的年科研费用和年利润具体数据如下表:
年科研费用 | 1 | 2 | 3 | 4 | 5 |
企业所获利润 | 2 | 3 | 4 | 4 | 7 |
(1)画出散点图;
(2)求![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(3)如果该企业某年研发费用投入8百万元,预测该企业获得年利润为多少?
参考公式:用最小二乘法求回归方程![]() 的系数
的系数![]() 计算公式:
计算公式:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解手机品牌的选择是否和年龄的大小有关,随机抽取部分华为手机使用者和苹果机使用者进行统计,统计结果如下表:
年龄 手机品牌 | 华为 | 苹果 | 合计 |
30岁以上 | 40 | 20 | 60 |
30岁以下(含30岁) | 15 | 25 | 40 |
合计 | 55 | 45 | 100 |
附:
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
根据表格计算得![]() 的观测值
的观测值![]() ,据此判断下列结论正确的是( )
,据此判断下列结论正确的是( )
A.没有任何把握认为“手机品牌的选择与年龄大小有关”
B.可以在犯错误的概率不超过0.001的前提下认为“手机品牌的选择与年龄大小有关”
C.可以在犯错误的概率不超过0.01的前提下认为“手机品牌的选择与年龄大小有关”
D.可以在犯错误的概率不超过0.01
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 是由到两个定点
是由到两个定点![]() 和点
和点![]() 的距离之积等于
的距离之积等于![]() 的所有点组成的.对于曲线
的所有点组成的.对于曲线![]() ,有下列四个结论:
,有下列四个结论:
①曲线![]() 是轴对称图形;
是轴对称图形;
②曲线![]() 是中心对称图形;
是中心对称图形;
③曲线![]() 上所有的点都在单位圆
上所有的点都在单位圆![]() 内;
内;
其中,所有正确结论的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据中国日报网报道:2017年11月13日,TOP500发布的最新一期全球超级计算机500强榜单显示,中国超算在前五名中占据两席,其中超算全球第一“神威太湖之光”完全使用了国产品牌处理器。为了了解国产品牌处理器打开文件的速度,某调查公司对两种国产品牌处理器进行了12次测试,结果如下(数值越小,速度越快,单位是MIPS)
测试1 | 测试2 | 测试3 | 测试4 | 测试5 | 测试6 | 测试7 | 测试8 | 测试9 | 测试10 | 测试11 | 测试12 | |
品牌A | 3 | 6 | 9 | 10 | 4 | 1 | 12 | 17 | 4 | 6 | 6 | 14 |
品牌B | 2 | 8 | 5 | 4 | 2 | 5 | 8 | 15 | 5 | 12 | 10 | 21 |
设![]() 分别表示第次测试中品牌A和品牌B的测试结果,记
分别表示第次测试中品牌A和品牌B的测试结果,记![]()
![]()
(Ⅰ)求数据![]() 的众数;
的众数;
(Ⅱ)从满足![]() 的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
(Ⅲ)经过了解,前6次测试是打开含有文字和表格的文件,后6次测试是打开含有文字和图片的文件.请你依据表中数据,运用所学的统计知识,对这两种国产品牌处理器打开文件的速度进行评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线关于![]() 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点![]() 、
、![]() 、
、![]() 均在抛物线上.
均在抛物线上.
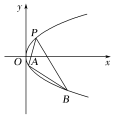
(1)写出该抛物线的方程及其准线方程;
(2)当![]() 与
与![]() 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求![]() 的值及直线
的值及直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com