
【题目】已知函数f(x)=loga|x+1|(a>0且a≠1),当x∈(0,1)时,恒有f(x)<0成立,则函数g(x)=loga(﹣ ![]() x2+ax)的单调递减区间是 .
x2+ax)的单调递减区间是 .
【答案】(0, ![]() ]
]
【解析】解:由题意:当x∈(0,1)时,|x+1|>1,但loga|x+1|<0,故由对数函数的图象知,0<a<1;
∵对数函数的真数要大于0,即﹣ ![]() x2+ax>0,解得:0<x<
x2+ax>0,解得:0<x< ![]() a,
a,
令t=﹣ ![]() x2+ax,开口向下,对称轴x=
x2+ax,开口向下,对称轴x= ![]() ,
,
当x在(0, ![]() ]时增函数,x在[
]时增函数,x在[ ![]() ,
, ![]() )时减函数.
)时减函数.
根据复合函数的单调性“同增异减”可得:
x∈(0,1)时,恒有f(x)<0成立时,函数g(x)=loga(﹣ ![]() x2+ax)的单调递减区间是(0,
x2+ax)的单调递减区间是(0, ![]() ].
].
故答案为:(0, ![]() ].
].
根据对数函数的性质可得当x∈(0,1)时,|x+1|>1,但loga|x+1|<0,故由对数函数的图象知,0<a<1.恒有f(x)<0成立,由﹣ ![]() x2+ax>0,解得0<x<
x2+ax>0,解得0<x< ![]() a,在根据复合函数的单调性即可得到答案.
a,在根据复合函数的单调性即可得到答案.


科目:高中数学 来源: 题型:
【题目】已知数列{an}是等比数列,且a2013+a2015= ![]() dx,则a2014(a2012+2a2014+a2016)的值为( )
dx,则a2014(a2012+2a2014+a2016)的值为( )
A.π2
B.2π
C.π
D.4π2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直三棱柱ABC﹣A1B1C1的侧面ACC1A1是正方形,AC=BC,点O是侧面ACC1A1的中心,∠ACB= ![]() ,M在棱BC上,且MC=2BM=2.
,M在棱BC上,且MC=2BM=2. 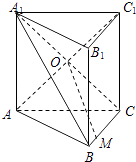
(1)证明BC⊥AC1;
(2)求OM的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (b≠0且b是常数).
(b≠0且b是常数).
(1)如果方程f(x)=x有唯一解,求b值.
(2)在(1)的条件下,求证:f(x)在(﹣∞,﹣1)上是增函数;
(3)若函数f(x)在(1,+∞)上是减函数,求负数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=ax在区间[0,2]上的最大值和最小值的和为5,则函数y=logax在区间[ ![]() ,2]上的最大值和最小值之差是( )
,2]上的最大值和最小值之差是( )
A.1
B.3
C.4
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com