
【题目】如图,在平面直角坐标系![]() 中,椭圆:
中,椭圆: ![]() 的离心率为
的离心率为![]() ,直线l:y=2上的点和椭圆上的点的距离的最小值为1.
,直线l:y=2上的点和椭圆上的点的距离的最小值为1.
(Ⅰ) 求椭圆的方程;
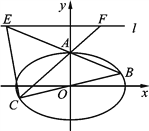
(Ⅱ) 已知椭圆的上顶点为A,点B,C是上的不同于A的两点,且点B,C关于原点对称,直线AB,AC分别交直线l于点E,F.记直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() .
.
① 求证: ![]() 为定值;
为定值;
② 求△CEF的面积的最小值.
【答案】(Ⅰ)![]() (Ⅱ)①详见解析②
(Ⅱ)①详见解析②![]()
【解析】试题分析:
(1)由题意求得![]() 的值,结合椭圆焦点位于
的值,结合椭圆焦点位于![]() 轴上写出标准方程即可;
轴上写出标准方程即可;
(2)①中,分别求得![]() 的值,然后求解其乘积即可证得结论;
的值,然后求解其乘积即可证得结论;
②中,联立直线与椭圆的方程,利用面积公式得出三角形面积的解析式,最后利用均值不等式求得面积的最小值即可.
试题解析:
(Ⅰ)由题知![]() ,由
,由![]() ,
,
所以![]() .
.
故椭圆的方程为![]() .
.
(Ⅱ)① 证法一:设![]() ,则
,则![]() ,
,
因为点B,C关于原点对称,则![]() ,
,
所以 .
.
证法二:直线AC的方程为![]() ,
,
由 得
得![]() ,
,
解得![]() ,同理
,同理![]() ,
,
因为B,O,C三点共线,则由![]() ,
,
整理得![]() ,
,
所以![]() .
.
②直线AC的方程为![]() ,直线AB的方程为
,直线AB的方程为![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
,
令y=2,得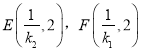 ,
,
而![]() ,
,
所以,△CEF的面积![]()
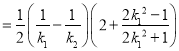
![]() .
.
由![]() 得
得![]() ,
,
则![]()
![]() ,当且仅当
,当且仅当![]() 取得等号,
取得等号,
所以△CEF的面积的最小值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】一企业从某条生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到如下的频率分布表:
x | [11,13) | [13,15) | [15,17) | [17,19) | [19,21) | [21,23) |
频数 | 2 | 12 | 34 | 38 | 10 | 4 |
(Ⅰ)作出样本的频率分布直方图,并估计该技术指标值x的平均数和众数;
(Ⅱ)若x<13或x≥21,则该产品不合格.现从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于13的产品恰有一件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在平面直角坐标系中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ) 求曲线![]() 与
与![]() 交点的平面直角坐标;
交点的平面直角坐标;
(Ⅱ) 点![]() 分别在曲线
分别在曲线![]() ,
, ![]() 上,当
上,当![]() 最大时,求
最大时,求![]() 的面积(
的面积(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,下列四组函数中表示相等函数的是( )
A.y=logax与y=(logxa)﹣1
B.y=2x与y=logaa2x
C.![]() 与y=x
与y=x
D.y=logax2与y=2logax
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)=  ,其中x是仪器的月产量.(注:总收益=总成本+利润)
,其中x是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润x表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的钢板的边界![]() 是抛物线的一部分,且
是抛物线的一部分,且![]() 垂直于抛物线对称轴,现欲从钢板上截取一块以
垂直于抛物线对称轴,现欲从钢板上截取一块以![]() 为下底边的等腰梯形钢板
为下底边的等腰梯形钢板![]() ,其中
,其中![]() 均在抛物线弧上.设
均在抛物线弧上.设![]() (米),且
(米),且![]() .
.
(1)当![]() 时,求等腰梯形钢板的面积;
时,求等腰梯形钢板的面积;
(2)当![]() 为何值时,等腰梯形钢板的面积最大?并求出最大值.
为何值时,等腰梯形钢板的面积最大?并求出最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com