
在一个花瓶中装有6枝鲜花,其中3枝山茶花,2枝杜鹃花和1枝君子兰,从中任取2枝鲜花.
(1)求恰有一枝山茶花的概率;
(2)求没有君子兰的概率.
(1)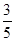 ;(2)
;(2)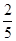 .
.
解析试题分析:本题是古典概型的概率计算问题,古典概型的概率计算,关键是计算出基本事件总数,某个事件发生时所包含的基本事件数,然后代入公式即可求解,本题采用列举法找出从6枝鲜花中任取2枝鲜花的所有可能有15种,对于(1)“恰有一枝山茶花”事件包含了9种基本事件,对于(2)“没有君子兰”事件则包含了10种基本事件,然后按照古典概率的计算公式进行计算即可.
试题解析:设3枝山茶花为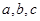 ,2枝杜鹃花为
,2枝杜鹃花为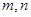 ,1枝君子兰为
,1枝君子兰为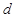 . 则从6枝鲜花中任取2枝的基本事件有:
. 则从6枝鲜花中任取2枝的基本事件有: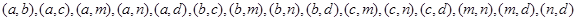 , 共15种 4分
, 共15种 4分
(1)其中恰有一枝山茶花的基本事件有: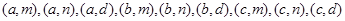 共9种,所以恰有一枝山茶花的概率为
共9种,所以恰有一枝山茶花的概率为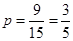 8分
8分
(2)其中没有君子兰的基本事件有: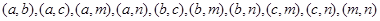 共10种,所以没有君子兰的概率为
共10种,所以没有君子兰的概率为 12分.
12分.
考点:古典概型的概率计算.


科目:高中数学 来源: 题型:解答题
某公司销售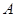 、
、 、
、 三款手机,每款手机都有经济型和豪华型两种型号,据统计
三款手机,每款手机都有经济型和豪华型两种型号,据统计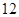 月份共销售
月份共销售 部手机(具体销售情况见下表)
部手机(具体销售情况见下表)
| | 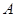 款手机 款手机 |  款手机 款手机 |  款手机 款手机 |
| 经济型 | 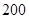 | 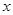 | 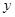 |
| 豪华型 | 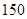 | 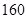 | 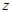 |
 部手机中,经济型
部手机中,经济型 款手机销售的频率是
款手机销售的频率是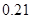 .
.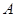 、
、 、
、 三款手机中抽取
三款手机中抽取 部,求在
部,求在 款手机中抽取多少部?
款手机中抽取多少部?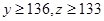 ,求
,求 款手机中经济型比豪华型多的概率.
款手机中经济型比豪华型多的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在打靶训练中,某战士射击一次的成绩在9环(包括9环)以上的概率是0.18,在8~9环(包括8环)的概率是0.51,在7~8环(包括7环)的概率是0.15,在6~7环(包括6环)的概率是0.09.计算该战士在打靶训练中射击一次取得8环(包括8环)以上成绩的概率和该战士打靶及格(及格指6环以上包括6环)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙、丙三人进行乒乓球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为 ,各局比赛的结果相互独立,第1局甲当裁判.
,各局比赛的结果相互独立,第1局甲当裁判.
(1)求第4局甲当裁判的概率;
(2)用X表示前4局中乙当裁判的次数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市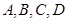 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
| 中学 | 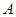 |  | 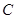 | 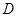 |
| 人数 | 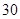 | 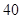 | 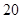 | 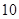 |
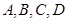 四所中学各抽取多少名学生?
四所中学各抽取多少名学生?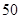 名学生中随机抽取两名学生,求这两名学生自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生自同一所中学的概率;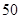 名学生中,从自
名学生中,从自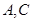 两所中学的学生当中随机抽取两名学
两所中学的学生当中随机抽取两名学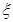 表示抽得
表示抽得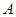 中学的学生人数,求
中学的学生人数,求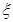 的分布列和期望.
的分布列和期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
佛山某中学高三(1)班排球队和篮球队各有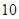 名同学,现测得排球队
名同学,现测得排球队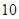 人的身高(单位:
人的身高(单位: )分别是:
)分别是: 、
、 、
、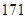 、
、 、
、 、
、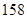 、
、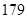 、
、 、
、 、
、 ,篮球队
,篮球队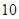 人的身高(单位:
人的身高(单位: )分别是:
)分别是: 、
、 、
、 、
、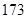 、
、 、
、 、
、 、
、 、
、 、
、 .
.
(Ⅰ) 请把两队身高数据记录在如图所示的茎叶图中,并指出哪个队的身高数据方差较小(无需计算);
(Ⅱ) 利用简单随机抽样的方法,分别在两支球队身高超过
 的队员中各抽取一人做代表,设抽取的两人中身高超过
的队员中各抽取一人做代表,设抽取的两人中身高超过
 的人数为
的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座。(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座的概率如下表: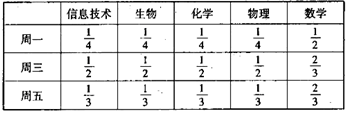
根据上表:
(Ⅰ)求数学辅导讲座在周一、周三、周五都不满座的概率;
(Ⅱ)设周三各辅导讲座满座的科目数为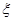 ,求随机变量
,求随机变量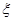 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一个盒子里装有4枝圆珠笔,其中3枝一等品,1枝三等品
(1)从盒子里任取2枝恰有1枝三等品的概率多大?
(2)从盒子里第一次任取1枝(不放回),第二次任取1枝;第一次取的是三等品,第二次取的是一等品的概率有多大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某次考试中,从甲,乙两个班各抽取10名学生的成绩进行统计分析,两班10名学生成绩的茎叶图如图所示,成绩不小于90分为及格.
(1)从每班抽取的学生中各抽取一人,求至少有一个及格的概率;
(2)从甲班10人中取两人,乙班10人中取一人,三人中及格人数记为X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com