
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若方程![]() 在区间
在区间![]() 内有解,求实数
内有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)函数![]() 的单调增区间是
的单调增区间是![]() ,单调减区间是
,单调减区间是![]() 和
和![]() .
.
(2)![]()
【解析】
(1)将![]() 代入解析式,求出
代入解析式,求出![]() ,利用导数与函数单调性的关系即可求解.
,利用导数与函数单调性的关系即可求解.
(2)由题意可知![]() ,其中
,其中![]() ,分类讨论
,分类讨论![]() 或
或![]() :当
:当![]() 时,利用导数判断出函数的单调性,再利用零点存在性定理即可判断有解;当
时,利用导数判断出函数的单调性,再利用零点存在性定理即可判断有解;当![]() 时,由
时,由![]() ,得
,得![]() ,分类讨论当
,分类讨论当![]() 或
或![]() ,利用导数判断函数的单调性,求出函数的最大值
,利用导数判断函数的单调性,求出函数的最大值![]() ,根据最大值结合函数的单调性即可求解.
,根据最大值结合函数的单调性即可求解.
解:(1)由题意可得![]()
则![]() ,
,
令![]() ,得
,得![]() ,
,![]()
当![]() 时,
时,![]() ,所以
,所以![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,所以
,所以![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,所以
,所以![]() 单调递减;
单调递减;
所以函数![]() 的单调增区间是
的单调增区间是![]() ,
,
单调减区间是![]() 和
和![]() .
.
(2)由题意可知![]() ,其中
,其中![]() ,
,
①当![]() 时,由于
时,由于![]() ,得
,得![]() ,故
,故![]() 在
在![]() 上为增函数,
上为增函数,
且![]() ,所以方程
,所以方程![]() 在
在![]() 有解;
有解;
②当![]() 时,由
时,由![]() ,得
,得![]() ,
,![]() (舍).
(舍).
(i)当![]() ,即
,即![]() 时,
时,
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
故![]() ,所以
,所以![]() 在
在![]() 上为减函数,
上为减函数,
所以![]() ,
,
所以此时方程![]() 在区间
在区间![]() 没有解;
没有解;
(ii)当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上为增函数,
上为增函数,
在![]() 上为减函数,所以当
上为减函数,所以当![]() 时,
时,
方程![]() 在区间
在区间![]() 才有解,
才有解,
而![]() ,
,
由![]() ,解得
,解得![]() 时,或
时,或![]() (不合题意,舍去),
(不合题意,舍去),
所以,当![]() 时,方程
时,方程![]() 在区间
在区间![]() 有解;
有解;
综上,当![]() 时,方程
时,方程![]() 在区间
在区间![]() 有解.
有解.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 是
是![]() 上一点.
上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是
是![]() 分别关于两坐标轴及坐标原点的对称点,平行于
分别关于两坐标轴及坐标原点的对称点,平行于![]() 的直线
的直线![]() 交
交![]() 于异于
于异于![]() 的两点
的两点![]() .点
.点![]() 关于原点的对称点为
关于原点的对称点为![]() .证明:直线
.证明:直线![]() 与
与![]() 轴围成的三角形是等腰三角形.
轴围成的三角形是等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在测试中,客观题难题的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:

测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
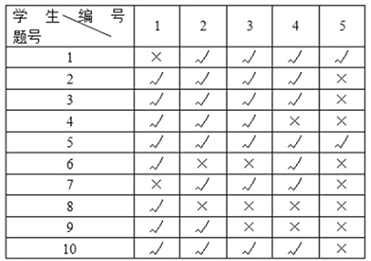
(1)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;

(2)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(3)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度, ![]() 为第
为第![]() 题的预估难度(
题的预估难度(![]() ).规定:若
).规定:若![]() ,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,...,39,40的40个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表(如下表)第1行的第4列和第5列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
60 44 66 44 21
66 06 58 05 62
61 65 54 35 02
42 35 48 96 32
14 52 41 52 48
92 66 22 15 86
96 63 75 41 99
58 42 36 72 24
A.23B.21C.35D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为实现有效利用扶贫资金,增加贫困村民的收入,扶贫工作组结合某贫困村水质优良的特点,决定利用扶贫资金从外地购买甲、乙、丙三种鱼苗在鱼塘中进行养殖试验,试验后选择其中一种进行大面积养殖,已知鱼苗甲的自然成活率为0.8.鱼苗乙,丙的自然成活率均为0.9,且甲、乙、丙三种鱼苗是否成活相互独立.
(1)试验时从甲、乙,丙三种鱼苗中各取一尾,记自然成活的尾数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)试验后发现乙种鱼苗较好,扶贫工作组决定购买![]() 尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.

(1)求出易倒伏玉米茎高的中位数![]() ;
;
(2)根据茎叶图的数据,完成下面的列联表:
抗倒伏 | 易倒伏 | |
矮茎 | ||
高茎 |
(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
附: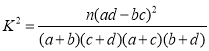 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在高一年级一班至六班进行了“社团活动”满意度调查(结果只有“满意”和“不满意”两种),从被调查的学生中随机抽取了50人,具体的调查结果如表:
班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
频数 | 4 | 5 | 11 | 8 | 10 | 12 |
满意人数 | 3 | 2 | 8 | 5 | 6 | 6 |
现从一班和二班调查对象中随机选取4人进行追踪调查,则选中的4人中恰有2人不满意的概率为___________;若将以上统计数据中学生持满意态度的频率视为概率,在高一年级全体学生中随机抽取3名学生,记其中满意的人数为X,则随机变量X的数学期望是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy上取两个定点A1(![]() ,0),A2(
,0),A2(![]() ,0),再取两个动点N1(0,m),N2(0,n),且mn=2.
,0),再取两个动点N1(0,m),N2(0,n),且mn=2.
(1)求直线A1N1与A2N2交点M的轨迹C的方程;
(2)过R(3,0)的直线与轨迹C交于P,Q,过P作PN⊥x轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若![]() (λ>1),求证:
(λ>1),求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为2,直线l与椭圆有且只有一个公共点.
,短轴长为2,直线l与椭圆有且只有一个公共点.
(1)求椭圆的方程;
(2)是否存在以原点O为圆心的圆满足:此圆与直线l相交于P,Q两点(两点均不在坐标轴上),且OP,OQ的斜率之积为定值,若存在,求出此定值和圆的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com