
分析 (1)以原点为圆心,椭圆C的短轴长为直径的圆与直线x-y+2=0相切,可得$\frac{2}{\sqrt{2}}$=b,解得b.又$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,a2=b2+c2,解出即可得出椭圆C的标准方程.
(2)设M(x0,y0),N(-x0,y0),可得直线PM的方程为:$y=\frac{{y}_{0}-1}{{x}_{0}}$x+1,直线QN的方程为:$y=\frac{{y}_{0}-2}{-{x}_{0}}$x+2,设T(x,y),联立基础代入椭圆方程即可得出.
解答 (1)解:∵以原点为圆心,椭圆C的短轴长为直径的圆与直线x-y+2=0相切,
∴$\frac{2}{\sqrt{2}}$=b,解得b=$\sqrt{2}$.
又$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,a2=b2+c2,解得a2=8,c=$\sqrt{6}$,
∴椭圆C的标准方程为:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1$.
(2)证明:设M(x0,y0),N(-x0,y0),可得直线PM的方程为:$y=\frac{{y}_{0}-1}{{x}_{0}}$x+1,直线QN的方程为:$y=\frac{{y}_{0}-2}{-{x}_{0}}$x+2,
设T(x,y),联立解得x0=$\frac{x}{2y-3}$,y0=$\frac{3y-4}{2y-3}$,
∵$\frac{{x}_{0}^{2}}{8}+\frac{{y}_{0}^{2}}{2}$=1,∴$\frac{1}{8}(\frac{x}{2y-3})^{2}$+$\frac{1}{2}(\frac{3y-4}{2y-3})^{2}$=1,
化为:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1$.
∴点T在椭圆上.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、直线与圆相切性质、点到直线的距离公式,考查了推理能力与计算能力,属于难题.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
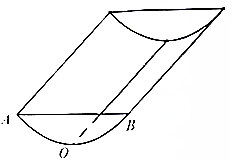 某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.
某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R | B. | ($\frac{1}{3}$,1) | C. | (0,$\frac{1}{3}$) | D. | (-∞,0]∪[$\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | [0,2] | C. | (0,2) | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{7}{25}$ | B. | $\frac{7}{25}$ | C. | $-\frac{24}{25}$ | D. | $\frac{24}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com