
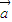 |=2|
|=2|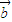 |≠0,且关于x的函数f(x)=
|≠0,且关于x的函数f(x)= x3+
x3+ |
| |x2+
|x2+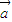 •
•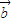 x在R上有极值,则
x在R上有极值,则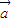 与
与 的夹角范围为 .
的夹角范围为 .  新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
(1)求点M的轨迹C的方程.
(2)是否存在直线l过点B(0,2),与轨迹C交于P、Q两点,且以PQ为直径的圆过原点?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
A.[0,![]() ] B.[
] B.[![]() ,
,![]() ] C.[
] C.[![]() ,
,![]() ] D.[
] D.[![]() ,
,![]() ]
]
查看答案和解析>>
科目:高中数学 来源:2015届云南省高一上学期期末考试数学试卷(解析版) 题型:选择题
已知|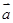 |=2|
|=2|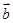 |≠0,且关于x的方程x2+|
|≠0,且关于x的方程x2+|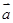 |x+
|x+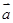 ·
·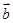 =0有实根,则
=0有实根,则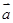 与
与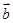 的夹角的取值范围是
的夹角的取值范围是
A.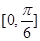 B.
B.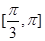 C.
C.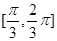 D.
D.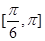
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com