
【题目】某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表:
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0. 15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在圆![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线段,
轴的垂线段, ![]() 为垂足,点
为垂足,点![]() 在线段
在线段![]() 上,且
上,且![]() ,点
,点![]() 在圆上运动。
在圆上运动。
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过定点![]() 的直线与点
的直线与点![]() 的轨迹交于
的轨迹交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为常数,若存在,求出点
为常数,若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三(1)班班主任李老师为了了解本班学生喜爱中国古典文学是否与性别有关,对全班50人进行了问卷调查,得到如下列联表:
喜欢中国古典文学 | 不喜欢中国古典文学 | 合计 | |
女生 | 5 | ||
男生 | 10 | ||
合计 | 50 |
已知从全班50人中随机抽取1人,抽到喜欢中国古典文学的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为喜欢中国古典文学与性别有关?请说明理由;
的把握认为喜欢中国古典文学与性别有关?请说明理由;
(3)已知在喜欢中国古典文学的10位男生中,![]() ,
,![]() ,
,![]() 还喜欢数学,
还喜欢数学,![]() ,
,![]() 还喜欢绘画,
还喜欢绘画,![]() ,
,![]() 还喜欢体育.现从喜欢数学、绘画和体育的男生中各选出1名进行其他方面的调查,求
还喜欢体育.现从喜欢数学、绘画和体育的男生中各选出1名进行其他方面的调查,求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
参考公式及数据:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节电方案,供电局对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照![]() ,
,![]() 分成9组,制成了如图所示的频率直方图.
分成9组,制成了如图所示的频率直方图.
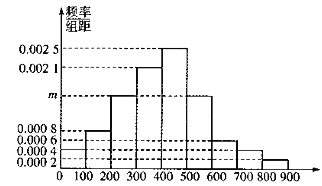
(1)求直方图中![]() 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;
(2)从样本里月均用电量不低于700度的用户中随机抽取4户,用![]() 表示月均用电量不低于800度的用户数,求随机变量
表示月均用电量不低于800度的用户数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校随机调查了80位学生,以研究学生中爱好羽毛球运动与性别的关系,得到下面的![]() 列联表:
列联表:
爱好 | 不爱好 | 合计 | |
男 | 20 | 30 | 50 |
女 | 10 | 20 | 30 |
合计 | 30 | 50 | 80 |
(Ⅰ)将此样本的频率估计为总体的概率,随机调查了本校的3名学生,设这3人中爱好羽毛球运动的人数为![]() ,求
,求![]() 的分布列,数学期望及方差;
的分布列,数学期望及方差;
(Ⅱ)根据表中数据,能否有充分证据判断爱好羽毛球运动与性别有关?若有,有多大把握?
| 0.500 | 0.100 | 0.050 | 0.010 |
| 0.455 | 2.706 | 3.841 | 6.635 |
附:
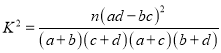
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com