
【题目】已知函数![]() ,有三个不同的零点,(其中
,有三个不同的零点,(其中![]() ),则
),则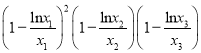 的值为( )
的值为( )
A. ![]() B.
B. ![]() C. -1 D. 1
C. -1 D. 1
【答案】D
【解析】令f(x)=0,分离参数得a=![]() 令h(x)=
令h(x)=![]() 由h′(x)=
由h′(x)=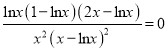 得x=1或x=e.
得x=1或x=e.
当x∈(0,1)时,h′(x)<0;当x∈(1,e)时,h′(x)>0;当x∈(e,+∞)时,h′(x)<0.
即h(x)在(0,1),(e,+∞)上为减函数,在(1,e)上为增函数.
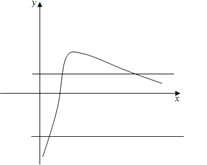
∴0<x1<1<x2<e<x3,a=![]() 令μ=
令μ=![]() 则a=
则a= ![]() 即μ2+(a-1)μ+1-a=0,
即μ2+(a-1)μ+1-a=0,
μ1+μ2=1-a<0,μ1μ2=1-a<0,
对于μ=![]() ,
, ![]() 则当0<x<e时,μ′>0;当x>e时,μ′<0.而当x>e时,μ恒大于0.不妨设μ1<μ2,则μ1=
则当0<x<e时,μ′>0;当x>e时,μ′<0.而当x>e时,μ恒大于0.不妨设μ1<μ2,则μ1=![]() ,
, 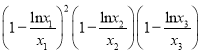 =(1-μ1)2(1-μ2)(1-μ3)
=(1-μ1)2(1-μ2)(1-μ3)
=[(1-μ1)(1-μ2)]2=[1-(1-a)+(1-a)]2=1.
故选D.


科目:高中数学 来源: 题型:
【题目】“扶贫帮困”是中华民族的传统美德,某校为帮扶困难同学,采用如下方式进行一次募捐:在不透明的箱子中放入大小均相同的白球七个,红球三个,每位献爱心的参与者投币20元有一次摸奖机会,一次性从箱子中摸球三个(摸完球后将球放回),若有一个红球,奖金10元,两个红球奖金20元,三个全是红球奖金100元.
(1)求献爱心参与者中将的概率;
(2)若该次募捐900位献爱心参与者,求此次募捐所得善款的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856332)
已知三棱柱ABC-A1B1C1如图所示,其中CA⊥平面ABB1A1,四边形ABB1A1为菱形,∠AA1B1=60°,E为BB1的中点,F为CB1的中点.
(Ⅰ)证明:平面AEF⊥平面CAA1C1;
(Ⅱ)若CA=2,AA1=4,求B1到平面AEF的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:f(x)=![]() 在区间(1,+∞)上是减函数;q:若x1,x2是方程x2-ax-2=0的两个实根,则不等式m2+5m-3≥|x1-x2|对任意实数a∈[-1,1]恒成立.若p不正确,q正确,求实数m的取值范围.
在区间(1,+∞)上是减函数;q:若x1,x2是方程x2-ax-2=0的两个实根,则不等式m2+5m-3≥|x1-x2|对任意实数a∈[-1,1]恒成立.若p不正确,q正确,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某读者协会为了了解该地区居民睡前看书的时间情况,从该地区睡前看书的居民中随机选取了n人进行调查,现将调查结果进行统计得到如图所示的频率分布直方图.则下列说法正确的是( )

A. 睡前看书时间介于40~50分钟的频率为0.03
B. 睡前看书时间低于30分钟的频率为0.67
C. 若n=1000,则可估计本次调查中睡前看书时间介于30~50分钟的有67人
D. 若n=1000,则可估计本次调查中睡前看书时间介于20~40分钟的有600人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为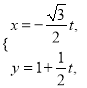 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,定点
,定点![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为
为![]() 的中点.
的中点.
(1)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,若
,若![]() 的中点为
的中点为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在标准温度和大气压下,人体血液中氢离子的物质的量的浓度(单位mol/L,记作![]() )和氢氧根离子的物质的量的浓度(单位mol/L,记作
)和氢氧根离子的物质的量的浓度(单位mol/L,记作![]() )的乘积等于常数
)的乘积等于常数![]() .已知pH值的定义为
.已知pH值的定义为![]() ,健康人体血液的pH值保持在7.35~7.45之间,那么健康人体血液中的
,健康人体血液的pH值保持在7.35~7.45之间,那么健康人体血液中的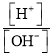 可以为(参考数据:
可以为(参考数据: ![]() ,
, ![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了鼓励学生热心公益,服务社会,成立了“慈善义工社”.2017年12月,该校“慈善义工社”为学生提供了4次参加公益活动的机会,学生可通过网路平台报名参加活动.为了解学生实际参加这4次活动的情况,该校随机抽取100名学生进行调查,数据统计如下表,其中“√”表示参加,“×”表示未参加.
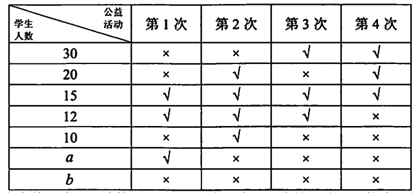
根据表中数据估计,该校4000名学生中约有120名这4次活动均未参加.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从该校4000名学生中任取一人,试估计其2017年12月恰参加了2次学校组织的公益活动的概率;
(Ⅲ)已知学生每次参加公益活动可获得10个公益积分,任取该校一名学生,记该生2017年12月获得的公益积分为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com