
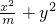 =1的左、右焦点分别为F1,F2,若椭圆上总存在点P,使得点P在以F1F2为直径的圆上;
=1的左、右焦点分别为F1,F2,若椭圆上总存在点P,使得点P在以F1F2为直径的圆上; (其中KAB、KOM分别表示直线AB、OM的斜率,O为坐标原点),求满足题意的椭圆C的方程.
(其中KAB、KOM分别表示直线AB、OM的斜率,O为坐标原点),求满足题意的椭圆C的方程. ,0),F2 (
,0),F2 ( ,0),
,0),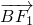 •
•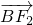 ≤0,
≤0, ,-1)•(
,-1)•( ,-1)=-(m-1)+1=2-m≤0,m≥2,
,-1)=-(m-1)+1=2-m≤0,m≥2, ∈[
∈[ ,1).
,1). ,
, ,
, =-(y1+y2)(y1-y2),
=-(y1+y2)(y1-y2), =
= ,又 KOM=
,又 KOM= ,
, ,m=4,此时,椭圆的方程为
,m=4,此时,椭圆的方程为 +y2=1.
+y2=1.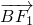 •
•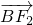 ≤0,由两个向量的数量积公式
≤0,由两个向量的数量积公式 ,求出 m值,即得椭圆的方程.
,求出 m值,即得椭圆的方程.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求△ABF2面积的最大值.
(2)求△ABF2面积取得最大值时tan∠F1AF2的值.
查看答案和解析>>
科目:高中数学 来源:2011年安徽省合肥市高考数学二模试卷(理科)(解析版) 题型:解答题
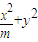 =1的左、右焦点分别为F1,F2,若椭圆上总存在点P,使得点P在以F1F2为直径的圆上;
=1的左、右焦点分别为F1,F2,若椭圆上总存在点P,使得点P在以F1F2为直径的圆上; (其中KAB、KOM分别表示直线AB、OM的斜率,O为坐标原点),求满足题意的椭圆C的方程.
(其中KAB、KOM分别表示直线AB、OM的斜率,O为坐标原点),求满足题意的椭圆C的方程.查看答案和解析>>
科目:高中数学 来源:2011年安徽省合肥市高考数学二模试卷(文科)(解析版) 题型:解答题
 =1的左、右焦点分别为F1,F2,若椭圆上总存在点P,使得点P在以F1F2为直径的圆上;
=1的左、右焦点分别为F1,F2,若椭圆上总存在点P,使得点P在以F1F2为直径的圆上; (其中KAB、KOM分别表示直线AB、OM的斜率,O为坐标原点),求满足题意的椭圆C的方程.
(其中KAB、KOM分别表示直线AB、OM的斜率,O为坐标原点),求满足题意的椭圆C的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com