
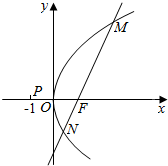
 已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.
已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.分析 (Ⅰ)求出M的坐标,代入抛物线方程,即可求抛物线C的方程;
(Ⅱ)分类讨论,利用韦达定理,结合斜率公式,即可得出结论.
解答  解:(Ⅰ)∵F为抛物线y2=2px(p>0)的焦点,
解:(Ⅰ)∵F为抛物线y2=2px(p>0)的焦点,
∴$F(\frac{p}{2},0)$.…(1分)
又∵l与x轴垂直,且|MN|=4,
∴$M(\frac{p}{2},2)$.…(2分)
又∵点M在抛物线上,
∴$4=2p×\frac{p}{2}={p^2}$,
∴p=2,
∴求抛物线C的方程为y2=4x.…(5分)
(Ⅱ)结论:k1+k2=0,为定值.
设直线l与抛物线交于不同两点M(x1,y1),N(x2,y2),
①当直线l斜率不存在时,知直线PM与PN关于x轴对称,
∴k1+k2=0.
②当直线l斜率存在时,直线l的方程设为y=k(x-1),
联立$\left\{\begin{array}{l}y=k(x-1)\\{y^2}=4x\end{array}\right.$,得k2x2-(2k2+4)x+k2=0,
∴${x_1}+{x_2}=\frac{{2{k^2}+4}}{k^2}$,x1x2=1.
又∵${k_1}=\frac{y_1}{{{x_1}+1}}$,${k_2}=\frac{y_2}{{{x_2}+1}}$,
且y1=k(x1-1),y2=k(x2-1),
∴${k_1}+{k_2}=\frac{y_1}{{{x_1}+1}}+\frac{y_2}{{{x_2}+1}}$=$\frac{{{y_1}({x_2}+1)+{y_2}({x_1}+1)}}{{({x_1}+1)({x_2}+1)}}$=$\frac{{k({x_1}-1)({x_2}+1)+k({x_2}-1)({x_1}+1)}}{{({x_1}+1)({x_2}+1)}}$=$\frac{{2k({x_1}{x_2}-1)}}{{{x_1}{x_2}+({x_1}+{x_2})+1}}$.
∵x1x2=1,
∴k1+k2=0.
综上所述k1+k2=0. …(14分)
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
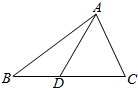 如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.
如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 45° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com