
分析 (1)将A和B点的坐标代入椭圆G的方程,列出方程组求出a和b的值,再求出c和离心率;
(2)由(1)求出椭圆G的方程,对直线l的斜率进行讨论,不妨设直线l的方程,与椭圆G的方程联立后,利用韦达定理写出式子,将条件转化为$\overrightarrow{AB}•\overrightarrow{AC}=0$,由向量数量积的坐标运算列出式子,代入化简后求出k的值,即得直线l的方程.
解答 解:(1)∵椭圆G过A(0,2),B(3,1),
∴$\left\{\begin{array}{l}{b=2}\\{\frac{9}{{a}^{2}}+\frac{1}{{b}^{2}}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2\sqrt{3}}\\{b=2}\end{array}\right.$,
则$c=\sqrt{{a}^{2}-{b}^{2}}$=$2\sqrt{2}$,
∴椭圆G的离心率e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$;
(2)由(1)得,椭圆G的方程是$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{4}=1$,
①当直线的斜率不存在时,则直线BC的方程是x=3,
代入椭圆G的方程得,C(3,-1),不符合题意;
②当直线的斜率存在时,设斜率为k,C(x1,y1),
则直线BC的方程为y=k(x-3)+1,
由$\left\{\begin{array}{l}{y=k(x-3)+1}\\{\frac{{x}^{2}}{12}+\frac{{y}^{2}}{4}=1}\end{array}\right.$得,(3k2+1)x2-6k(3k-1)x+27k2-18k-3=0,
∴3+x1=$\frac{6k(3k-1)}{3{k}^{2}+1}$,3x1=$\frac{3(9{k}^{2}-6k-1)}{3{k}^{2}+1}$,则x1=$\frac{9{k}^{2}-6k-1}{3{k}^{2}+1}$,
∵以BC为直径圆经过点A,
∴AB⊥AC,则$\overrightarrow{AB}•\overrightarrow{AC}=0$,即(3,-1)•(x1,y1-2)=0,
∴3x1-y1+2=0,即3x1-[k(x1-3)+1]=0,
∴(3-k)x1+3k+1=0,(3-k)•$\frac{9{k}^{2}-6k-1}{3{k}^{2}+1}$+3k+1=0,
化简得,18k2-7k-1=0,
解得k=$-\frac{1}{2}$ 或k=$\frac{1}{9}$,
∴直线BC的方程为y=$-\frac{1}{2}$(x-3)+1或y=$\frac{1}{9}$(x-3)+1,
即直线BC的方程是x+2y-5=0或x-9y+6=0,
综上得,直线l的方程是x+2y-5=0或x-9y+6=0.
点评 本题考查了待定系数法求椭圆标准方程,直线与椭圆位置关系,向量数量积的坐标运算,以及“设而不求”的解题思想方法,考查转化思想,化简、变形、计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
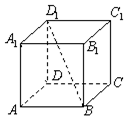 如图,在正方形ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,
如图,在正方形ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\vec a-2\vec b$ | B. | $\overrightarrow{a}$-4$\vec b$ | C. | $\vec a$ | D. | $\vec b$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com