
【题目】如图1,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() 在线段
在线段![]() 上,且
上,且![]() 。将
。将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到
到![]() 的位置(如图2所示),且
的位置(如图2所示),且![]() 。
。
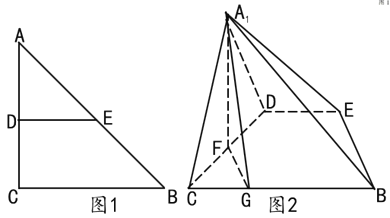
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
【答案】(1)证明见解析
(2)![]()
【解析】
(1)要证明线面平行,需证明线线平行,取![]() 的中点
的中点![]() ,连接
,连接![]() ,根据条件证明
,根据条件证明![]() ,即
,即![]() ;
;
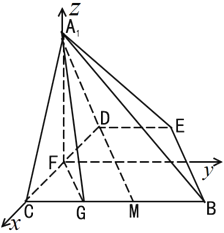
(2)以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,过
轴,过![]() 作平行于
作平行于![]() 的直线为
的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,求两个平面的法向量,利用法向量求二面角的余弦值.
,求两个平面的法向量,利用法向量求二面角的余弦值.
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
∵![]() ,∴
,∴![]() 为
为![]() 的中点.
的中点.
又![]() 为
为![]() 的中点,∴
的中点,∴![]() .
.
依题意可知![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,从而
,从而![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,
![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,
,
![]() 以
以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,过
轴,过![]() 作平行于
作平行于![]() 的直线为
的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,不妨设
,不妨设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则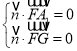 ,即
,即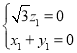 ,
,
令![]() ,得
,得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则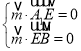 ,即
,即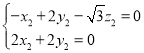 ,
,
令![]() ,得
,得![]() .
.
从而![]() ,
,
故平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】绿水青山就是金山银山.近年来,祖国各地依托本地自然资源,打造旅游产业,旅游业正蓬勃发展.景区与游客都应树立尊重自然、顺应自然、保护自然的生态文明理念,合力使旅游市场走上规范有序且可持续的发展轨道.某景区有一个自愿消费的项目:在参观某特色景点入口处会为每位游客拍一张与景点的合影,参观后,在景点出口处会将刚拍下的照片打印出来,游客可自由选择是否带走照片,若带走照片则需支付20元,没有被带走的照片会收集起来统一销毁.该项目运营一段吋间后,统计出平均只有三成的游客会选择带走照片,为改善运营状况,该项目组就照片收费与游客消费意愿关系作了市场调研,发现收费与消费意愿有较强的线性相关性,并统计出在原有的基础上,价格每下调1元,游客选择带走照片的可能性平均增加0.05,假设平均每天约有5000人参观该特色景点,每张照片的综合成本为5元,假设每个游客是否购买照片相互独立.
(1)若调整为支付10元就可带走照片,该项目每天的平均利润比调整前多还是少?
(2)要使每天的平均利润达到最大值,应如何定价?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列A:![]() ,
,![]() ,…
,…![]() (
(![]() ).如果对小于
).如果对小于![]() (
(![]() )的每个正整数
)的每个正整数![]() 都有
都有![]() <
<![]() ,则称
,则称![]() 是数列A的一个“G时刻”.记“
是数列A的一个“G时刻”.记“![]() 是数列A的所有“G时刻”组成的集合.
是数列A的所有“G时刻”组成的集合.
(1)对数列A:-2,2,-1,1,3,写出![]() 的所有元素;
的所有元素;
(2)证明:若数列A中存在![]() 使得
使得![]() >
>![]() ,则
,则![]() ;
;
(3)证明:若数列A满足![]() -
-![]() ≤1(n=2,3, …,N),则
≤1(n=2,3, …,N),则![]() 的元素个数不小于
的元素个数不小于![]() -
-![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 的定义域为
的定义域为![]() ,且存在实常数a,使得对于定义域内任意x,都
,且存在实常数a,使得对于定义域内任意x,都![]() 成立,则称此函数
成立,则称此函数![]() 具有“
具有“![]() 性质”
性质”
(1)判断函数![]() 是否具有“
是否具有“![]() 性质”,若具有“
性质”,若具有“![]() 性质”,求出所有a的值的集合;若不具有“
性质”,求出所有a的值的集合;若不具有“![]() 性质”,请说明理由;
性质”,请说明理由;
(2)已知函数![]() 具有“
具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(3)已知函数![]() 具有“
具有“![]() 性质”,又具有“
性质”,又具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,若函数
,若函数![]() 的图像与直线
的图像与直线![]() 有2017个公共点,求实数p的值.
有2017个公共点,求实数p的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)过椭圆 上异于其顶点的任意一点Q作圆
上异于其顶点的任意一点Q作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在x轴,y轴上的截距分别为
在x轴,y轴上的截距分别为![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)若![]() 是椭圆
是椭圆![]() 上不同两点,
上不同两点,![]() 轴,圆E过
轴,圆E过![]() ,且椭圆
,且椭圆![]() 上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆
上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆![]() 是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的极值;
的极值;
(2)问:是否存在实数![]() ,使得
,使得![]() 有两个相异零点?若存在,求出
有两个相异零点?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于
的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于![]() ,直线l与椭圆C交于
,直线l与椭圆C交于![]() 两点.
两点.
(1)求椭圆C的方程;
(2)过点O作直线l的垂线,垂足为D.若![]() ,求动点D的轨迹方程.
,求动点D的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com